
����Ŀ��ijУ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ����Ϊ����֪���١���ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ���dz��˽⡱�����Ƚ��˽⡱���������˽⡱������̫�˽⡱�ĸ��ȼ����ֱ����![]() ��
��![]() ��
��![]() ��
��![]() �������ݵ��������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��δ��ɣ�������ͼ��������Ϣ����������⣺
�������ݵ��������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��δ��ɣ�������ͼ��������Ϣ����������⣺
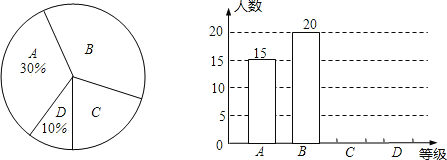
��1���α������ѧ�����ж����ˣ���������ͳ��ͼ������ͳ��ͼ����������
��2���ڡ��Ƚ��˽⡱�ĵ�����������꼶ѧ������5�ˣ�����2��3Ů������5���У��������ѡ��2λ���вɷã��������б�������״ͼ�ķ��������ѡ��λͬѧ������һλ����ͬѧ�ĸ��ʣ�
���𰸡���1��50����ͼ�����������2��![]() .
.
��������
��1����������ͳ��ͼ������ͳ��ͼ��A��������ٷֱȼ�����������������������C��D���������������ͳ��ͼ�����������ɣ�
��2������ͼ���ó���5λͬѧ��ѡ��λͬѧ�ĵȿ��ܽ������20�֣������ó�����Ҫ��Ľ����������ʼ��ɣ�
�⣺��1�����α������ѧ�����У�![]() ���ˣ���
���ˣ���![]() �ˣ�
�ˣ�![]() ���ˣ�.
���ˣ�.
��ȫͳ��ͼ���£�
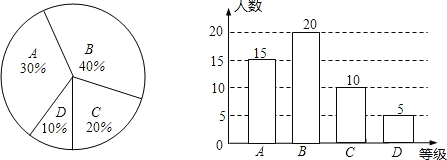
��2���б����£�
��1 | ��2 | Ů1 | Ů2 | Ů3 | |
��1 | ����1����2�� | ����1��Ů1�� | ����1��Ů2�� | ����1��Ů3�� | |
��2 | ����2����1�� | ����2��Ů1�� | ����2��Ů2�� | ����2��Ů3�� | |
Ů1 | ��Ů1����1�� | ��Ů1����2�� | ��Ů1��Ů2�� | ��Ů1��Ů3�� | |
Ů2 | ��Ů2����1�� | ��Ů2����2�� | ��Ů2��Ů1�� | ��Ů2��Ů3�� | |
Ů3 | ��Ů3����1�� | ��Ů3����2�� | ��Ů3��Ů1�� | ��Ů3��Ů2�� |
�ɱ���֪������20�ֵȿ��ܵĽ��������������һ����ͬѧ�Ľ����14�֣�
����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�·ݵ�Ӫҵ��Ϊ200��Ԫ��һ�¡����¡����µ�Ӫҵ�1000��Ԫ�����ƽ��ÿ��������Ϊ![]() �����������з���ӦΪ____________________________ ��
�����������з���ӦΪ____________________________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2���ڷ���ax2+bx+c=0����������x1=��1��x2=3��
��3a+c=0���ܵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3���ݵ�x��0ʱ��y��x������������н�����ȷ����_____��ֻ������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ȵ���������֮��.Ϊ�˵�����Уѧ��������ȫ֪ʶˮƽ��ѧУ��֯��һ��ȫУ��������ȫ֪ʶ��ѵ����ѵ�����в��ԣ���ȫУ2400��ѧ���У��ֱ��ȡ��������Ů����15�ݳɼ������������������£��벹������.
���ռ����ݣ�
����15��ѧ�����Գɼ�ͳ�����£�
68��72��89��85��82��85��74��92��80��85��76��85��69��78��80
Ů��15��ѧ�����Գɼ�ͳ�����£�(����100��)
82��88��83��76��73��78��67��81��82��80��80��86��82��80��82
�����·����������������������������ݣ�
��� Ƶ�� | 65.5��70.5 | 70.5��75.5 | 75.5��80.5 | 80.5��85.5 | 85.5��90.5 | 90.5��95.5 |
���� | 2 | 2 | 4 | 5 | 1 | 1 |
�� | 1 | 1 | 5 | 6 | 2 | 0 |
���������ݣ�
(1)�����������ݵ�ƽ��������������λ�����������±���ʾ��
�༶ | ƽ���� | ���� | ��λ�� | ���� |
���� | 80 | x | 80 | 45.9 |
�� | 80 | 82 | y | 24.3 |
�ڱ��У�x��_____��y��_____.
(2)���涨�÷���80������(����80��)Ϊ�ϸ������ȫУѧ����������ȫ֪ʶ�ϸ��ѧ����______��.
(3)ͨ�����ݷ����õ��Ľ�����Ů������������ȫ���֪ʶ������ˮƽ�������ã������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
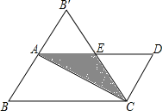
����Ŀ����ͼ����ƽ���ı���ֽƬ![]() �У�
�У�![]() ����ֽƬ�ضԽ���
����ֽƬ�ضԽ���![]() ���ۣ�
���ۣ�![]() ����
����![]() �߽��ڵ�
�߽��ڵ�![]() ����ʱ��
����ʱ��![]() ǡΪ�ȱ������Σ����ص����Ϊ�� ��
ǡΪ�ȱ������Σ����ص����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ���ľߣ�����Ϊ5Ԫ/�����ۼ�Ϊ6Ԫ/��ʱ�������������Ϊ100���������۹����з��֣��ۼ�ÿ����0.5Ԫ��������������ͼ���5�����赱�����۵���ͳһΪ![]() Ԫ/����
Ԫ/����![]() ����
����![]() �ǰ�0.5Ԫ�ı������ǣ���������������Ϊ
�ǰ�0.5Ԫ�ı������ǣ���������������Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() �ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2��Ҫʹ��������������240Ԫ���������۵������ڵķ�Χ��
��3����ÿ���ľߵ�������![]() ��Ҫ�뵱�����������ÿ���ľ��ۼ�Ϊ����Ԫ��������������
��Ҫ�뵱�����������ÿ���ľ��ۼ�Ϊ����Ԫ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���������⣺
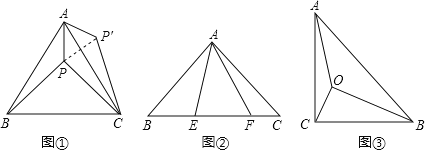
��1����ͼ�ٵȱߡ�ABC����һ��P������P������A��B��C�ľ���ֱ�Ϊ3��4��5�����APB�Ķ�����
Ϊ�˽�����⣬���ǿ��Խ���ABP�ƶ���A��ת����ACP��������ʱ��ACP���ա�ABP�������Ϳ���������ת�任���������߶�PA��PB��PCת����һ���������У��Ӷ������APB��__________��
��2����������
�������õڣ�1����Ľ��˼�뷽��������������⣺
��֪��ͼ�ڣ���ABC�У���CAB��90����AB��AC��E��FΪBC�ϵĵ��ҡ�EAF��45������֤��EF2��BE2+FC2��
��3����������
��ͼ�ۣ���Rt��ABC�У���C��90����AC��1����ABC��30������OΪRt��ABC��һ�㣬����AO��BO��CO���ҡ�AOC����COB����BOA��120������OA+OB+OC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y����x2+bx+c��ͼ����A����1��0����C��0��3��.
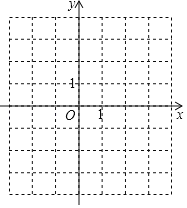
��1������κ����Ľ���ʽ��
��2����ͼ�У��������κ�����ͼ��
��3������ͼ��ֱ��д����y��0ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������y=ax2+bx����ƽ��2����λ֮��,������x�ύ��A(-3,0),B(1,0)����,��y�ύ�ڵ�C.
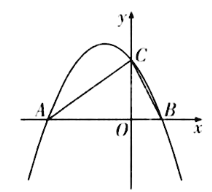
(1)��ƽ�ƺ������ߵı���ʽ;
(2)��Q��ֱ��AC�Ϸ�����������һ��,����Q��QE��ֱ��x��,���Ե�B��Q��EΪ����Ľ�������AOC����,�����Q�������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com