
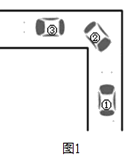
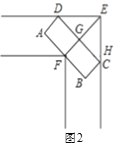
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
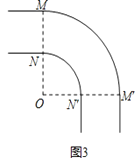
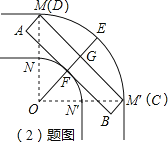
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
【答案】(1)消防车不能通过该直角转弯;(2)ON至少为4.5米.
【解析】
(1)过点F作FH⊥EC于点H,根据道路的宽度求出FH=EH=4m,然后根据等腰直角三角形的性质求出EF、GE的长度,相减即可得到GF的长度,如果不小于车身宽度,则消防车能通过,否则,不能通过;
(2)假设车身C、D分别与点M′、M重合,根据等腰直角三角形的性质求出OG=![]() CD=4,OC=
CD=4,OC=![]() CG=4
CG=4![]() ,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG=
,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG=![]() CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.
CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.
解:(1)消防车不能通过该直角转弯.
理由如下:如图,作FH⊥EC,垂足为H,
∵FH=EH=4,
∴EF=4![]() ,且∠GEC=45°,
,且∠GEC=45°,
∵GC=4,
∴GE=GC=4,
∴GF=4![]() ﹣4<3,
﹣4<3,
即GF的长度未达到车身宽度,
∴消防车不能通过该直角转弯.
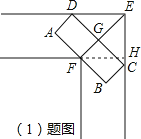
(2)若C、D分别与M′、M重合,则△OGM为等腰直角三角形,
∴OG=4,OM=4![]() ,
,
∴OF=ON=OM﹣MN=4![]() ﹣4,
﹣4,
∴FG=OG﹣OF=![]() ×8﹣(4
×8﹣(4![]() ﹣4)=8﹣4
﹣4)=8﹣4![]() <3,
<3,
∴C、D在![]() 上,
上,
设ON=x,连接OC,在Rt△OCG中,
OG=x+3,OC=x+4,CG=4,
由勾股定理得,OG2+CG2=OC2,
即(x+3)2+42=(x+4)2,
解得x=4.5.
答:ON至少为4.5米.


科目:初中数学 来源: 题型:
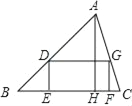
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用.某商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡为每个进价45元,售价为每个60元,普通白炽灯泡进价为每个25元,售价为每个30元.
(1)若LED灯泡按原售价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元.求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)该商场又购进LED灯泡与普通白炽灯泡若干个并展开了降价促销活动,在促销期间,每个LED灯泡的利润为进价的(m+20)%,每个普通白炽灯泡按原售价降低![]() m%销售.结果在促销活动中LDE灯泡的销售量比(1)中的销售量降低了
m%销售.结果在促销活动中LDE灯泡的销售量比(1)中的销售量降低了![]() m%,普通白炽灯泡销售量比(1)中销售量上升了20%,活动共获利2400元,求m的值.
m%,普通白炽灯泡销售量比(1)中销售量上升了20%,活动共获利2400元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx+a-5(a、b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象经过点(-1,4),求该二次函数的解析式.
(2)无论a取何常数,这个二次函数的图象始终经过一个定点,求出这个定点坐标.
(3)已知点P(x0,m)和Q(1,n)都在二次函数的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
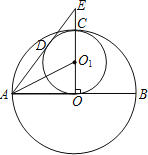
【题目】 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1=_____,DE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
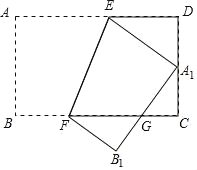
【题目】如图,将矩形ABCD沿EF对折,点A1恰好落在CD边上的中点处,线段A1B1交BC于点G,若AB=6,AD=9,则CG的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
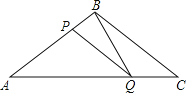
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)当![]() ,求
,求![]() 的值;
的值;
(3)![]() 能否与
能否与![]() 相似?若能,求出
相似?若能,求出![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
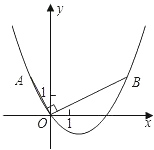
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com