
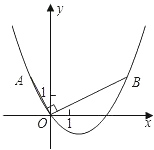
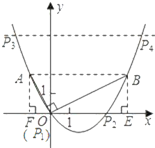
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
【答案】(1)B(4,2);(2)![]() ;(3)P 1 (0,0),P 2 (3,0),
;(3)P 1 (0,0),P 2 (3,0),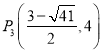 ,
,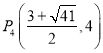
【解析】
(1) 过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x 轴,垂足为点E,则AF=2,OF=1,再证明Rt△AFO∽Rt△OEB,根据相似三角形的性质求得BE=2,OE=4,即可得点B的坐标为(4,2);(2)利用待定系数法求得抛物线的解析式即可;(3)根据三角形的面积公式求得点P的纵坐标只能是0或4,再解方程即可求得点P的坐标.
(1)如图,过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x 轴,垂足为点E,则AF=2,OF=1,
∵OA⊥OB,
∴∠AOF+∠BOE=90°,
又∵∠BOE+∠OBE=90°,
∴∠AOF=∠OBE,
∴Rt△AFO∽Rt△OEB,
∵OB=2OA,
∴![]() ,
,
∴BE=2,OE=4,
∴B(4,2);
(2)设过点A(-1,2),B(4,2),0(0,0)的抛物线为y=ax2 +bx,
∴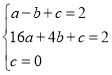 ,
,
解得,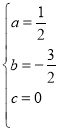 ,
,
∴所求抛物线的表达式为![]() ;
;
(3)∵A (-1,2),B(4,2),
∴AB∥x轴,
设抛物线上符合条件的点P到AB的距离为d,
则S△ABP =![]() ,∴d=2,
,∴d=2,
∴点P的纵坐标只能是0或4,
令y=0,得![]() ,解之,得x=0,或x=3,
,解之,得x=0,或x=3,
∴符合条件的点P1 (0,0),P 2 (3,0),
令y=4,得![]() ,解之,得
,解之,得![]() ,
,
∴符合条件的点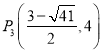 ,
,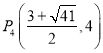 ,
,
∴综上,符合题意的点有四个:P 1 (0,0),P 2 (3,0),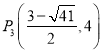 ,
,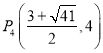 .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
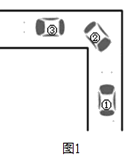
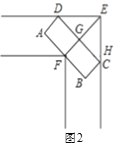
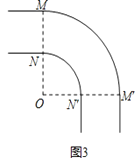
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
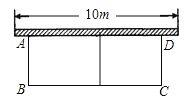
【题目】如图,有长为18米的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为Sm2.
(1)求S与x的函数关系式,并写出x的取值范围;
(2)如果要围成面积为24m2的花圃,AB的长是多少米?
(3)能围成面积比24m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】强哥驾驶小汽车(出租)匀速地从如皋火车站送客到南京绿口机场,全程为280km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数解析式;
(2)强哥上午8点驾驶小汽车从如皋火车站出发.
①乘客需在当天10点48分至11点30分(含10点48分和11点30分)间到达南京绿口机场,求小汽车行驶速度v的范围;
②强哥能否在当天10点前到达绿口机场?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
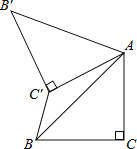
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
(1)求∠ABC'的度数;
(2)求C'B的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
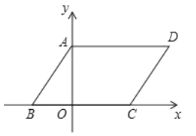
【题目】如图,在平面直角坐标系中,四边形![]() 是平行四边形,
是平行四边形,![]() ,若
,若![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
(1)直接写出:![]() ______,
______,![]() ______;
______;
(2)若点![]() 为
为![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ;
;
①求经过![]() ,
,![]() 两点的直线解析式;
两点的直线解析式;
②求证:![]() .
.
(3)若点![]() 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,直接写出
为顶点的四边形为菱形?若存在,直接写出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )
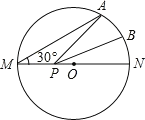
A.2B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
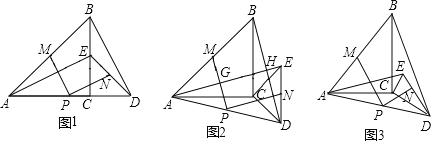
(1)请直接写出PM与PN的数量关系及位置关系 ;
(2)现将图1中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图2,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系 ;
(3)若图2中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图3,写出PM与PN的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com