
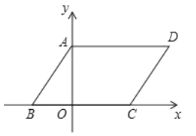
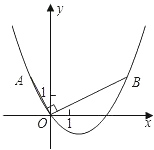
【题目】如图,在平面直角坐标系中,四边形![]() 是平行四边形,
是平行四边形,![]() ,若
,若![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
(1)直接写出:![]() ______,
______,![]() ______;
______;
(2)若点![]() 为
为![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ;
;
①求经过![]() ,
,![]() 两点的直线解析式;
两点的直线解析式;
②求证:![]() .
.
(3)若点![]() 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,直接写出
为顶点的四边形为菱形?若存在,直接写出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
【答案】(1)4,3;(2)①![]() ;,②证明见解析;(3)
;,②证明见解析;(3)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)解一元二次方程求出OA,OB的长度即可;
(2)先根据三角形的面积求出点E的坐标,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.
(1)方程![]() ,
,
分解因式得:![]() ,
,
可得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ;
;
故答案为4,3;
(2)①根据题意,设![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴点![]() 的坐标是
的坐标是![]() ,
,
设经过![]() 、
、![]() 两点的直线的解析式为
两点的直线的解析式为![]() ,
,
则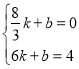 ,
,
解得: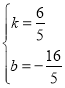 ,
,
∴解析式为![]() ;
;
②如图,
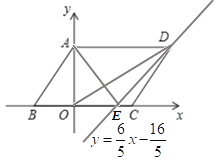
在![]() 与
与![]() 中,
中,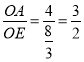 ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)根据计算的数据,![]() ,
,
∵![]() ,
,
∴![]() 平分
平分![]() ,
,
分四种情况考虑:
①![]() 、
、![]() 是邻边,点
是邻边,点![]() 在射线
在射线![]() 上时,
上时,![]() ,
,
∴点![]() 与
与![]() 重合,即
重合,即![]() ;
;
②![]() 、
、![]() 是邻边,点
是邻边,点![]() 在射线
在射线![]() 上时,
上时,![]() 应在直线
应在直线![]() 上,且
上,且![]() 垂直平分
垂直平分![]() ,
,
此时点![]() 坐标为
坐标为![]() ;
;
③![]() 是对角线时,做
是对角线时,做![]() 垂直平分线
垂直平分线![]() ,
,![]() 解析式为
解析式为![]() ,直线
,直线![]() 过
过![]() ,且
,且![]() 值为
值为![]() (平面内互相垂直的两条直线
(平面内互相垂直的两条直线![]() 值乘积为-1),
值乘积为-1),
∴![]() 解析式为
解析式为![]() ,
,
联立直线![]() 与直线
与直线![]() ,得:
,得: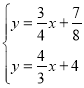 ,
,
解得:![]() ,
,![]() ,
,
∴![]() ;
;
④![]() 是对角线时,过
是对角线时,过![]() 作
作![]() 垂线,垂足为
垂线,垂足为![]() ,
,
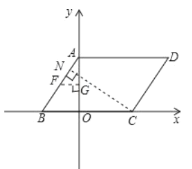
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得![]() ,即
,即![]() ,
,
做![]() 关于
关于![]() 的对称点,记为
的对称点,记为![]() ,
,![]() ,
,
过![]() 做
做![]() 轴垂线,垂足为
轴垂线,垂足为![]() ,
,![]() ,
,
∴![]() ,
,
综上所述,满足条件的点有四个:![]() ;
;![]() ;
;![]() ;
;![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次测量旗杆高度的活动中,某数学兴趣小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB,CD,EF都垂直于地面,若AB=1.6米,CD=2米,人与标杆之间的距离BD=1米,标杆与旗杆之间的距离DF=30米,求旗杆EF的高.
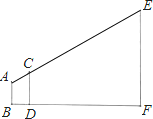
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家的阳台上放置了一个晒衣架如图①.图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面.经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖落到地面上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2019个正方形的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒局上经常两人玩猜拳游戏.游戏规则是:每人同时伸出一只手的几个手指(手指数可以是0、1、2、3、4、5),并同时口中喊出一个数,若某人喊出的数恰好等于两人的手指数的和,而另一个人喊出的数与两人的手指数的和不等,就算喊对的人赢,输的人就要喝酒,两人都喊对了或都没喊对,就重来.在某次甲乙两人猜拳时,甲说:“我让让你,我就喊一个数5,其他的数我都不喊,都归你喊,如何?”请你用学过的概率知识加以分析,试说明甲是否作出了让步.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com