
【题目】如图1,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
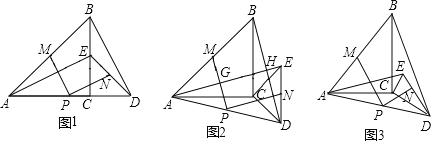
(1)请直接写出PM与PN的数量关系及位置关系 ;
(2)现将图1中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图2,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系 ;
(3)若图2中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图3,写出PM与PN的数量关系,并加以证明.
【答案】(1)PM=PN,PM⊥PN,理由见解析;(2)PM=PN,PM⊥PN,理由见解析;(3)PM=kPN,证明见解析.
【解析】
(1)利用等腰直角三角形的性质得出结论判断出△ACE≌△BCD,得出AE=BD,再用三角形的中位线即可得出结论;
(2)同(1)的方法即可得出结论;
(3)利用两边对应成比例夹角相等,判断出△BCD∽△ACE,得出BD=kAE,最后用三角形的中位线即可得出结论.
解:(1)PM=PN,PM⊥PN,
理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中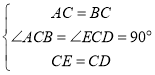 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵∠BCD=90°,
∴∠CBD+∠BDC=90°,
∴∠EAC+∠BDC=90°
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM=![]() BD,PN=
BD,PN=![]() AE,
AE,
∴PM=PN,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM∥BC,PN∥AE,
∴∠NPD=∠EAC,∠MPN=∠BDC,
∵∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN,
故答案为:PM⊥PN,PM=PN;
(2)PM=PN,PM⊥PN,
理由:∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS).
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=![]() BD,PM∥BD;
BD,PM∥BD;
PN=![]() AE,PN∥AE.
AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN.
故答案为:PM⊥PN,PM=PN;
(3)PM=kPN,
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴![]() =k.
=k.
∴△BCD∽△ACE.
∴BD=kAE,
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=![]() BD,PN=
BD,PN=![]() AE.
AE.
∴PM=kPN.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
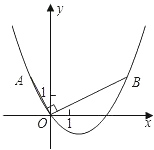
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为![]() m,DC的长为
m,DC的长为![]() m。
m。
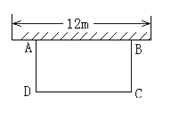
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量![]() 能否取值为4m,若能,求出
能否取值为4m,若能,求出![]() 的值,若不能,请说明理由;
的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒局上经常两人玩猜拳游戏.游戏规则是:每人同时伸出一只手的几个手指(手指数可以是0、1、2、3、4、5),并同时口中喊出一个数,若某人喊出的数恰好等于两人的手指数的和,而另一个人喊出的数与两人的手指数的和不等,就算喊对的人赢,输的人就要喝酒,两人都喊对了或都没喊对,就重来.在某次甲乙两人猜拳时,甲说:“我让让你,我就喊一个数5,其他的数我都不喊,都归你喊,如何?”请你用学过的概率知识加以分析,试说明甲是否作出了让步.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.三角形ABC的三个顶点均在格点上,以点A为圆心的弧EF与BC相切于格点D,分别交AB,AC于点E,F.
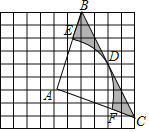
(1)直接写出三角形ABC边长AB= ;AC= ;BC= .
(2)求图中由线段EB,BC,CF及弧FE所围成的阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
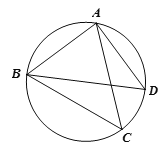
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com