
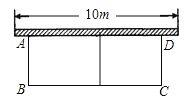
【题目】如图,有长为18米的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为Sm2.
(1)求S与x的函数关系式,并写出x的取值范围;
(2)如果要围成面积为24m2的花圃,AB的长是多少米?
(3)能围成面积比24m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)AB的长为4米;(3)能围成面积比24m2更大的花圃,最大面积是27m2,此时AB=3m,BC=9m.
;(2)AB的长为4米;(3)能围成面积比24m2更大的花圃,最大面积是27m2,此时AB=3m,BC=9m.
【解析】
(1)先用x表示出BC,再利用矩形的面积解答即可,利用![]() 即可求出x的取值范围;
即可求出x的取值范围;
(2)根据题意,当(1)题中的S=24时,求出x的值即可;
(3)根据(1)中的函数的性质结合自变量的取值范围解答即可.
解:(1)根据题意,得:![]() ,∴
,∴![]() ,
,
∵墙的最大可用长度为10米,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴x的取值范围是:![]() ;
;
(2)当S=24时,![]() ,解得:
,解得:![]() ,
,![]() ,
,
∵![]() ,∴x=4,即AB=4,
,∴x=4,即AB=4,
∴要围成面积为24m2的花圃,AB的长为4米;
(3)![]() ,
,
∵![]() ,且-3<0,
,且-3<0,
∴当x=3时有最大面积的花圃,为27 m2,
∴能围成面积比24m2更大的花圃,最大面积是27m2,此时AB=3m,BC=9m.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用.某商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡为每个进价45元,售价为每个60元,普通白炽灯泡进价为每个25元,售价为每个30元.
(1)若LED灯泡按原售价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元.求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)该商场又购进LED灯泡与普通白炽灯泡若干个并展开了降价促销活动,在促销期间,每个LED灯泡的利润为进价的(m+20)%,每个普通白炽灯泡按原售价降低![]() m%销售.结果在促销活动中LDE灯泡的销售量比(1)中的销售量降低了
m%销售.结果在促销活动中LDE灯泡的销售量比(1)中的销售量降低了![]() m%,普通白炽灯泡销售量比(1)中销售量上升了20%,活动共获利2400元,求m的值.
m%,普通白炽灯泡销售量比(1)中销售量上升了20%,活动共获利2400元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
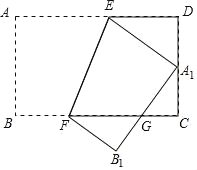
【题目】如图,将矩形ABCD沿EF对折,点A1恰好落在CD边上的中点处,线段A1B1交BC于点G,若AB=6,AD=9,则CG的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
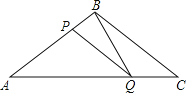
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿着
点出发,沿着![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动;同时点
点运动;同时点![]() 从
从![]() 点出发,沿
点出发,沿![]() 以每秒
以每秒![]() 的速度向
的速度向![]() 点运动,设运动时间为
点运动,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)当![]() ,求
,求![]() 的值;
的值;
(3)![]() 能否与
能否与![]() 相似?若能,求出
相似?若能,求出![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0)
(1)求证:无论m为任何非0实数,此方程总有两个实数根.
(2)若抛物线y=mx2+(1﹣5m)x﹣5(m≠0)与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
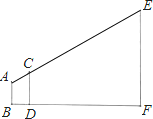
【题目】在一次测量旗杆高度的活动中,某数学兴趣小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB,CD,EF都垂直于地面,若AB=1.6米,CD=2米,人与标杆之间的距离BD=1米,标杆与旗杆之间的距离DF=30米,求旗杆EF的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
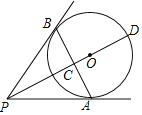
A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的表达式;
(3)连接AB,在(2)中的抛物线上是否存在点P,使得S△ABP=S△ABO.若存在,请直接写出点P的坐标
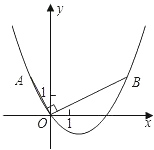
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com