
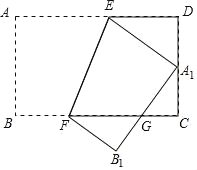
【题目】如图,将矩形ABCD沿EF对折,点A1恰好落在CD边上的中点处,线段A1B1交BC于点G,若AB=6,AD=9,则CG的长度为______.
【答案】![]()
【解析】
由折叠的性质可得AE=A1E,A1D=3=A1C,∠EA1G=90°,由勾股定理可得DE=4,通过证明△A1DE∽△CGA1,可得![]() ,可求CG的长.
,可求CG的长.
解:如图,
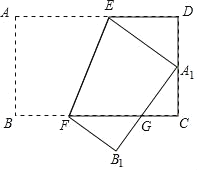
∵四边形ABCD是矩形,
∴AB=CD=6,∠D=∠C=90°
∵将矩形ABCD沿EF对折,点A1恰好落在CD边上的中点处,
∴AE=A1E,A1D=3=A1C,∠EA1G=90°,
∵A1E2=DE2+A1D2,
∴(9﹣DE)2=DE2+9,
∴DE=4,
∵∠DEA1+∠DA1E=90°,∠EA1D+∠GA1C=90°,
∴∠DEA1=∠GA1C,∠D=∠C=90°
∴△A1DE∽△CGA1,
∴![]()
∴![]() ,
,
∴GC=![]() .
.
故答案为:![]()


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
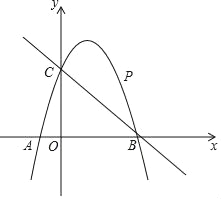
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
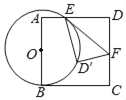
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
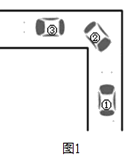
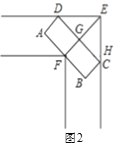
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
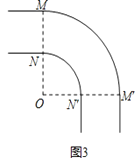
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
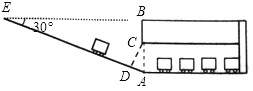
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.
(1)试求该校地下停车场的高度AC;
(2)求CD的高度,一辆高为6米的车能否通过该地下停车场(![]() =1.73,结果精确到0.1米).
=1.73,结果精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1y2,其中y1=![]() +1,y2=
+1,y2=![]() x﹣1,请对该函数及其图象进行如下探究:
x﹣1,请对该函数及其图象进行如下探究:
解析式探究:根据给定的条件,可以确定出该函数的解析式为:______.
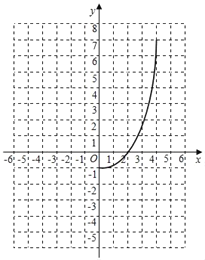
函数图象探究:①根据解析式,完成下表:
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m=______,n=_____.
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出当x≤0时的函数图象;
结合画出的函数图象,解决问题:
①若A(x1,y1)、B(x2,y2)为图象上的两点,满足x1<x2;则y1_____y2(用<、=、>填空).
②写出关于x的方程y1y2=﹣x+3的近似解(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.

(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
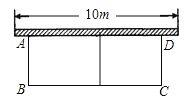
【题目】如图,有长为18米的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为Sm2.
(1)求S与x的函数关系式,并写出x的取值范围;
(2)如果要围成面积为24m2的花圃,AB的长是多少米?
(3)能围成面积比24m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com