
【题目】如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
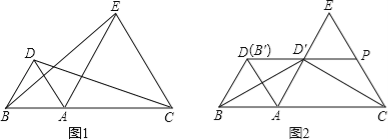
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.
【答案】解:(1)见详解;(2)① 60;②当AC=2AB时,△BDD′与△CPD′全等.理由见详解.
【解析】
(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,然后求出∠BAE=∠DAC,再利用“边角边”证明△BAE和△DAC全等,根据全等三角形对应边相等即可得证;
(2)①求出∠DAE,即可得到旋转角度数;
②当AC=2AB时,△BDD′与△CPD′全等.根据旋转的性质可得AB=BD=DD′=AD′,然后得到四边形ABDD′是菱形,根据菱形的对角线平分一组对角可得∠ABD′=∠DBD′=30°,菱形的对边平行可得DP∥BC,根据等边三角形的性质求出AC=AE,∠ACE=60°,然后根据等腰三角形三线合一的性质求出∠PCD′=∠ACD′=30°,从而得到∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PD′C=30°,然后利用“角边角”证明△BDD′与△CPD′全等.
(1)证明:∵△ABD和△ACE都是等边三角形
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
在△BAE和△DAC中,
 ,
,
∴△BAE≌△DAC(SAS),
∴BE=CD;
(2)①∵∠BAD=∠CAE=60°,
∴∠DAE=180°60°×2=60°,
∵边AD′落在AE上,
∴旋转角=∠DAE=60°.
故答案为:60.
②当AC=2AB时,△BDD′与△CPD′全等.
理由如下:由旋转可知,AB′与AD重合,
∴AB=BD=DD′=AD′,
∴四边形ABDD′是菱形,
∴∠ABD′=∠DBD′=![]() ∠ABD=12×60°=30°,DP∥BC,
∠ABD=12×60°=30°,DP∥BC,
∵△ACE是等边三角形,
∴AC=AE,∠ACE=60°,
∵AC=2AB,
∴AE=2AD′,
∴∠PCD′=∠ACD′=![]() ∠ACE=
∠ACE=![]() ×60°=30°,
×60°=30°,
又∵DP∥BC,
∴∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PCD′=∠PD′C=30°,
在△BDD′与△CPD′中,
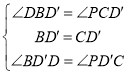 ,
,
∴△BDD′≌△CPD′(ASA).


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
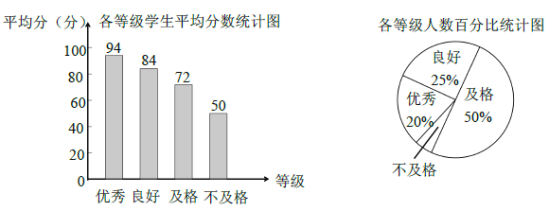
【题目】《中学生体质健康标准》规定学生体质健康等级标准为:90分及以上为优秀;80分~89分为良好;60分~79分为及格;59分及以下为不及格. 某校从九年级学生中随机抽取了![]() 的学生进行了体质测试,得分情况如下图.
的学生进行了体质测试,得分情况如下图.
(1)在抽取的学生中不及格人数所占的百分比是 ,它的圆心角度数为 度.
(2)小明按以下方法计算出抽取的学生平均得分是:![]() . 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
. 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
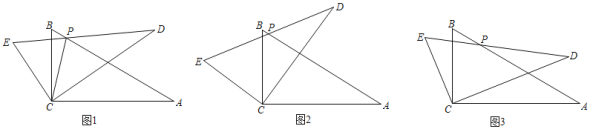
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.

(1)画出旋转后的小旗A′C′D′B′;
(2)写出点A′,C′,D′的坐标;
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
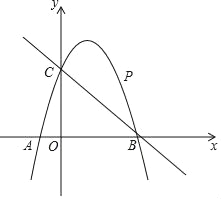
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个被等分成8个扇形的转盘.请在扇形内写上“红、黑”表示涂上相应的颜色,未写表示白色,使得自由转动停止后,指针落在红色区域的概率等于落在黑色区域的概率,且小于落在白色区域的概率.填出两种,再指出“红、黑,白”分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示,![]() ),村委会想在
),村委会想在![]() 地带与
地带与![]() 地带种植单价为10元的太阳花,当
地带种植单价为10元的太阳花,当![]() 地带种满花后,已经花了500元,请你计算一下,若继续在
地带种满花后,已经花了500元,请你计算一下,若继续在![]() 地带种植同样的太阳花,资金是否够用?并说明理由.
地带种植同样的太阳花,资金是否够用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1y2,其中y1=![]() +1,y2=
+1,y2=![]() x﹣1,请对该函数及其图象进行如下探究:
x﹣1,请对该函数及其图象进行如下探究:
解析式探究:根据给定的条件,可以确定出该函数的解析式为:______.
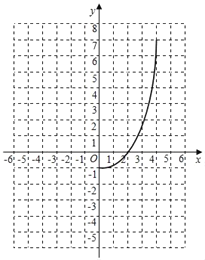
函数图象探究:①根据解析式,完成下表:
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m=______,n=_____.
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出当x≤0时的函数图象;
结合画出的函数图象,解决问题:
①若A(x1,y1)、B(x2,y2)为图象上的两点,满足x1<x2;则y1_____y2(用<、=、>填空).
②写出关于x的方程y1y2=﹣x+3的近似解(精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com