
【题目】在汛期到来之际,某水泵厂接到生产一批小型抽水泵的紧急任务。要求必须在10天内(含10天)完成任务。为提高生产效率,工厂加班加点,接到任务的第一天就生产了水泵20台,以后每天生产的水泵都比前一天多2 台。由于机器损耗等原因,当日生产的水泵数量达到28台后,每多生产一台,当天生产的所有水泵,平均每台成本就增加20元。
(1)设第![]() 天生产水泵
天生产水泵![]() 台,直接写出
台,直接写出![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若每台水泵的成本价(日生产量不超过28台时)为1000元,销售价格为每台1400元,设第![]() 天的利润为
天的利润为![]() 元,试求
元,试求![]() 与
与![]() 之间的函数解析式,并求该厂哪一天获得的利润最大,最大利润最多少?
之间的函数解析式,并求该厂哪一天获得的利润最大,最大利润最多少?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
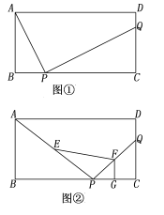
【题目】已知:如图①,②,在矩形ABCD中,AB=4,BC=8,P,Q分别是边BC,CD上的点.
(1)如图①,若AP⊥PQ,BP=2,求CQ的长;
(2)如图②,若![]() =2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
=2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2﹣2x+c的部分图象如图1所示:
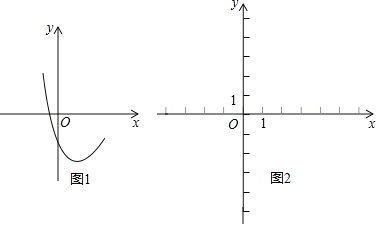
(1)确定c的取值范围;
(2)若抛物线经过点(0,﹣1),试确定抛物线y1=x2﹣2x+c的解析式;
(3)若反比例函数y2=![]() 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象写出当y1>y2时,对应自变量x的取值范围.
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象写出当y1>y2时,对应自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
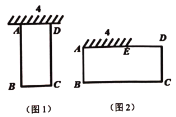
【题目】如图,校园空地上有一面墙,长度为4米,为了创建“美丽校园”,学校决定借用这面墙和20米的围栏围成一个矩形花园![]() ,设
,设![]() 长为
长为![]() 米,矩形花园
米,矩形花园![]() 的面积为
的面积为![]() 平方米.
平方米.
(1)如图1,若所围成的矩形花园![]() 边的长不得超出这面墙,求
边的长不得超出这面墙,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,当![]() 为何值时,矩形花园
为何值时,矩形花园![]() 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)如图2,若围成的矩形花园![]() 的
的![]() 边的长可超出这面墙,求围成的矩形
边的长可超出这面墙,求围成的矩形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
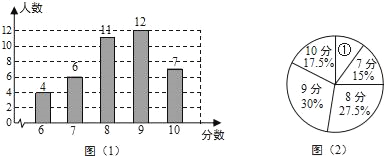
(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,直线 y=kx+b 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
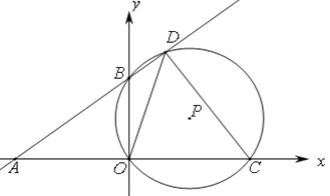
(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=![]() , 求点D的坐标.
, 求点D的坐标.
(3)当△ODC为等腰三角形时,求出所有符合条件的m的值.
(4)点P,Q关于OD成轴对称,当点Q恰好落在直线AB上时,直接写出此时BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
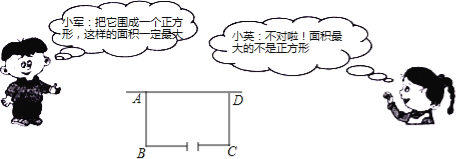
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com