
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 首先根据抛物线与x轴交于两个不同点可得到b2-4ac>0,根据抛物线的顶点坐标公式为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴x=x=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{b}{2a}$来进行判断.
解答 解:由二次函数y=ax2+bx+c(a≠0)与x轴交于两个不同点A(x1,0),B(x2,0),
∴b2-4ac>0,故①正确;
由二次函数化为顶点式是y=a(x-h)2+k,可知x=$\frac{{x}_{1}+{x}_{2}}{2}$=h,
∴x1+x2=2h,故②正确;
由二次函数y=ax2+bx+c(a≠0)化为顶点式是y=a(x-h)2+k可知:-$\frac{b}{2a}$=h,$\frac{4ac-{b}^{2}}{4a}$=k,
∴二次函数y=ax2+bx+2c的顶点横坐标为:-$\frac{b}{2a}$=h,纵坐标为:$\frac{4a×2c-{b}^{2}}{4a}$=$\frac{8ac-{b}^{2}}{4a}$≠2k,故③错误;
∵$\frac{4ac-{b}^{2}}{4a}$=k,c=k,
∴$\frac{4ac-{b}^{2}}{4a}$=c,解得b=0,
∴h=-$\frac{b}{2a}$=0,故④正确;
因此正确的结论是①②④.
故答案为:C.
点评 本题主要考查对二次函数图象与系数的关系,抛物线与x轴的交点,二次函数顶点的坐标特征等知识点的理解和掌握.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
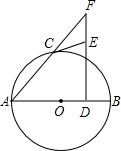 如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E.
如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F.过点C作⊙O的切线交FD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )
如图,小明用自制的直角三角形纸板DEF测量树AB的高度,测量时,使直角边DF保持水平状态,其延长线交AB于点G;使斜边DE所在的直线经过点A.测得边DF离地面的高度为1m,点D到AB的距离等于7.5m.已知DF=1.5m,EF=0.6m,那么树AB的高度等于( )| A. | 4m | B. | 4.5m | C. | 4.6m | D. | 4.8m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
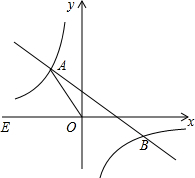 在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.
在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?为什么?
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com