
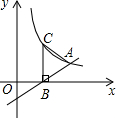
 如图,直线y=$\frac{1}{2}$x-1与x轴交于点B,与双曲线y=$\frac{k}{x}$(x>0)交于点A,过点B作x轴的垂线,与双曲线y=$\frac{k}{x}$交于点C.且AB=AC,则k的值为4.
如图,直线y=$\frac{1}{2}$x-1与x轴交于点B,与双曲线y=$\frac{k}{x}$(x>0)交于点A,过点B作x轴的垂线,与双曲线y=$\frac{k}{x}$交于点C.且AB=AC,则k的值为4. 分析 根据题目中的信息,可以用含k的式子表示点C的坐标,由AB=AC,可知点A在线段BC的垂直平分线上,从而可以得到点A的纵坐标,从而可以表示出点A的坐标,又由点A在直线y=$\frac{1}{2}$x-1上,可以得到k的值,本题得以解决.
解答 解:∵直线y=$\frac{1}{2}$x-1与x轴交于点B,
∴当y=0时,x=2,
∴点B的坐标为(2,0),
又∵过点B作x轴的垂线,与双曲线y=$\frac{k}{x}$交于点C,
∴点C的坐标为(2,$\frac{k}{2}$),
∵AB=AC,
∴点A在线段BC的垂直平分线上,
∴点A的纵坐标为$\frac{k}{4}$,
∵点A在双曲线y=$\frac{k}{x}$上,
∴$\frac{k}{4}=\frac{k}{x}$,得x=4,
又∵点A(4,$\frac{k}{4}$)在直线y=$\frac{1}{2}$x-1上,
∴$\frac{k}{4}=\frac{1}{2}×4-1$
解得k=4.
故答案为:4.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,灵活变化,认真推导.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
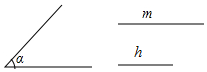 (1)已知∠α和线段m,h,用直尺和圆规作?ABCD,使AB=m,∠DAB=∠α,AB和CD之间的距离为h(作出图形,不写作法,保留痕迹)
(1)已知∠α和线段m,h,用直尺和圆规作?ABCD,使AB=m,∠DAB=∠α,AB和CD之间的距离为h(作出图形,不写作法,保留痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
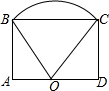 如图,点O是矩形ABCD的边AD的中点,以O为圆心画$\widehat{BC}$,一个动点P从O出发沿线段OA→线段AB→$\widehat{BC}$→线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )
如图,点O是矩形ABCD的边AD的中点,以O为圆心画$\widehat{BC}$,一个动点P从O出发沿线段OA→线段AB→$\widehat{BC}$→线段CD→线段DO作匀速运动,最后回到点O,设OP=y,运动时间为x,则y关于x的函数图象可能是( )| A. | 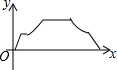 | B. | 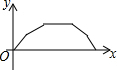 | C. | 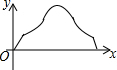 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
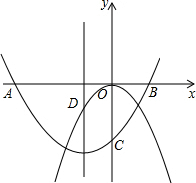 如图,在平面直角坐标系xOy中,把抛物线C1:y=-x2沿x轴翻折,再平移得到抛物线C2,恰好经过点A(-3,0)、B(1,0),抛物线C2与y轴交于点C,抛物线C1:y=-x2与抛物线C2的对称轴交于D点.
如图,在平面直角坐标系xOy中,把抛物线C1:y=-x2沿x轴翻折,再平移得到抛物线C2,恰好经过点A(-3,0)、B(1,0),抛物线C2与y轴交于点C,抛物线C1:y=-x2与抛物线C2的对称轴交于D点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
某地4月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )| A. | 19,19 | B. | 19,19.5 | C. | 21,22 | D. | 20,20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com