
【题目】如图为二次函数y=ax2+bx+c的图象,给出下列说法:其中正确的说法有__. ①ab>0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x>1时,随x值的增大而增大.
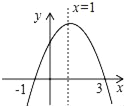
【答案】②③.
【解析】
①由抛物线的开口向下,对称轴在y轴的右侧,判断a,b与0的关系,得到ab<0;故①错误;
②由抛物线与x轴的交点坐标得到方程ax2+bx+c=0的根为x1=﹣1,x2=3;故②正确;
③由x=1时,得到y=a+b+c>0;故③正确;
④根据对称轴x=1,得到当x>1时,随x值的增大而减小,故错误.
①∵抛物线的开口向下,∴a<0.
∵对称轴在y轴的右侧,∴b>0,∴ab<0,故①错误;
②∵抛物线与x轴交于(﹣1,0),(3,0),∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,故②正确;
③当x=1时,a+b+c>0,故③正确;
④当x>1时,随x值的增大而减小,故错误.
故答案为:②③.


科目:初中数学 来源: 题型:
【题目】在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
则m、n的大小关系为( )
A. m>n B. m<n C. m=n D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.
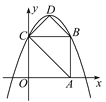
查看答案和解析>>
科目:初中数学 来源: 题型:
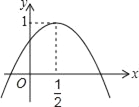
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(![]() ,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
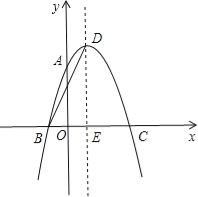
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目:初中数学 来源: 题型:
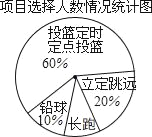
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
请你根据图表中的信息回答下列问题:
(1) 训练后篮球定时定点投篮人均进球数为 个;
(2) 选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3) 根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+![]() ,则下列结论:
,则下列结论:
(1)柱子OA的高度为![]() m;
m;
(2)喷出的水流距柱子1m处达到最大高度;
(3)喷出的水流距水平面的最大高度是2.5m;
(4)水池的半径至少要2.5m才能使喷出的水流不至于落在池外.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com