
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
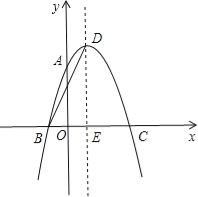
【答案】(1)抛物线解析式为y=﹣x2+2x+3;
(2)BD=![]() .
.
【解析】
试题(1)将A与B代入抛物线解析式求出a与c的值,即可确定出抛物线解析式;
(2)利用顶点坐标公式表示出D坐标,进而确定出E坐标,得到DE与OE的长,根据B坐标求出BO的长,进而求出BE的长,在直角三角形BED中,利用勾股定理求出BD的长.
试题解析:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得:![]() ,
,
解得:![]() ,
,
则抛物线解析式为y=﹣x2+2x+3;
(2)由D为抛物线顶点,得到D(1,4),
∵抛物线与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD=![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列五个结论中:①albic<0;②a﹣b+c>0;③2a﹣b<0;④abc<0;⑤4a+2b+c>0,错误的个数有( )
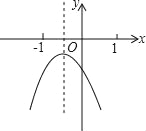
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
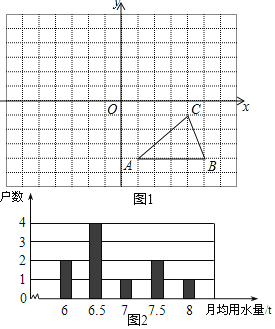
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )
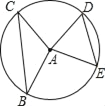
A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:
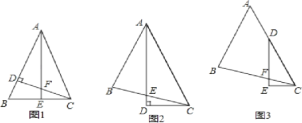
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用80万元![]() 万元只计入第一年成本
万元只计入第一年成本![]() ,成功研发出一种产品
,成功研发出一种产品![]() 公司按订单生产
公司按订单生产![]() 产量
产量![]() 销售量
销售量![]() ,第一年该产品正式投产后,生产成本为6元
,第一年该产品正式投产后,生产成本为6元![]() 件
件![]() 此产品年销售量
此产品年销售量![]() 万件
万件![]() 与售价
与售价![]() 元
元![]() 件
件![]() 之间满足函数关系式
之间满足函数关系式![]() .
.
![]() 求这种产品第一年的利润
求这种产品第一年的利润![]() 万元
万元![]() 与售价
与售价![]() 元
元![]() 件
件![]() 满足的函数关系式;
满足的函数关系式;
![]() 该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
![]() 第二年,该公司将第一年的利润20万元
第二年,该公司将第一年的利润20万元![]() 万元只计入第二年成本
万元只计入第二年成本![]() 再次投入研发,使产品的生产成本降为5元
再次投入研发,使产品的生产成本降为5元![]() 件
件![]() 为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件
为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件![]() 请计算该公司第二年的利润
请计算该公司第二年的利润![]() 至少为多少万元.
至少为多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com