
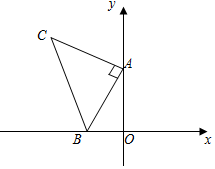
 如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).分析 (1)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=2,AE=BO=1,即可得出点C的坐标;
(2)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=a,AE=BO=1,可得OE=a=1,即可得出点C的坐标为(-a,a+1),据此可得c+d的值不变;
(3)分为三种情况讨论,分别画出符合条件的图形,构造直角三角形,证出三角形全等,根据全等三角形对应边相等即可得出答案;
解答  解:(1)如图,过点C作CE⊥y轴于E,则∠CEA=∠AOB,
解:(1)如图,过点C作CE⊥y轴于E,则∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,
∴∠ACE+∠CAE=90°=∠BAO+∠CAE,
∴∠ACE=∠BAO,
在△ACE和△BAO中,
$\left\{\begin{array}{l}{∠CEA=∠AOB}\\{∠ACE=∠BAO}\\{AC=BA}\end{array}\right.$,
∴△ACE≌△BAO(AAS),
∵B(-1,0),A(0,2),
∴BO=AE=1,AO=CE=2,
∴OE=1+2=3,
∴C(-2,3),
故答案为:-2,3;
(2)动点A在运动的过程中,c+d的值不变.
过点C作CE⊥y轴于E,则∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,
∴∠ACE+∠CAE=90°=∠BAO+∠CAE,
∴∠ACE=∠BAO,
在△ACE和△BAO中,
$\left\{\begin{array}{l}{∠CEA=∠AOB}\\{∠ACE=∠BAO}\\{AC=BA}\end{array}\right.$,
∴△ACE≌△BAO(AAS),
∵B(-1,0),A(0,a),
∴BO=AE=1,AO=CE=a,
∴OE=1+a,
∴C(-a,1+a),
又∵点C的坐标为(c,d),
∴c+d=-a+1+a=1,即c+d的值不变;
(3)存在一点P,使△PAB与△ABC全等,
分为三种情况:
①如图,过P作PE⊥x轴于E,则∠PBA=∠AOB=∠PEB=90°,
∴∠EPB+∠PBE=90°,∠PBE+∠ABO=90°,
∴∠EPB=∠ABO,
在△PEB和△BOA中,
$\left\{\begin{array}{l}{∠EPB=∠ABO}\\{∠PEB=∠BOA}\\{PB=BA}\end{array}\right.$,
∴△PEB≌△BOA(AAS),
∴PE=BO=1,EB=AO=2,
∴OE=2+1=3,
即P的坐标是(-3,1);
②如图,过C作CM⊥x轴于M,过P作PE⊥x轴于E, 则∠CMB=∠PEB=90°,
则∠CMB=∠PEB=90°,
∵△CAB≌△PAB,
∴∠PBA=∠CBA=45°,BC=BP,
∴∠CBP=90°,
∴∠MCB+∠CBM=90°,∠CBM+∠PBE=90°,
∴∠MCB=∠PBE,
在△CMB和△BEP中,
$\left\{\begin{array}{l}{∠MCB=∠PBE}\\{∠CMB=∠PEB}\\{BC=BP}\end{array}\right.$,
∴△CMB≌△BEP(AAS),
∴PE=BM,CM=BE,
∵C(-2,3),B(-1,0),
∴PE=1,OE=BE-BO=3-1=2,
即P的坐标是(2,1);
③如图,过P作PE⊥x轴于E, 则∠BEP=∠BOA=90°,
则∠BEP=∠BOA=90°,
∵△CAB≌△PBA,
∴AB=BP,∠CAB=∠ABP=90°,
∴∠ABO+∠PBE=90°,∠PBE+∠BPE=90°,
∴∠ABO=∠BPE,
在△BOA和△PEB中,
$\left\{\begin{array}{l}{∠ABO=∠BBPE}\\{∠BOA=∠PEB}\\{BA=BP}\end{array}\right.$,
∴△BOA≌△PEB(AAS),
∴PE=BO=1,BE=OA=2,
∴OE=BE-BO=2-1=1,
即P的坐标是(1,-1),
综合上述,符合条件的P的坐标是(-3,1)或(2,1)或(1,-1).
点评 本题属于三角形综合题,主要考查了全等三角形的性质和判定,三角形内角和定理,等腰直角三角形性质的应用,考核了学生综合运用性质进行推理的能力,解决问题的关键是作辅助线构造全等三角形以及运用运用分类讨论的思想.


科目:初中数学 来源: 题型:解答题
| 累计购物 实际花费 | 500 | 700 | … | x |
| 在甲商场 | 400 | 560 | … | 0.8x |
| 在乙商场 | 410 | 550 | … | 0.7x+60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com