
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( ) 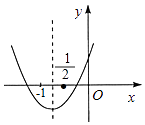
A.1
B.2
C.3
D.4
【答案】C
【解析】解:由图象可知,a>0,b>0,c>0, ∵﹣ ![]() >﹣1,
>﹣1,
∴b<2a,故①正确,
假如|a﹣b+c|<c,
则∵a﹣b+c<0,
∴﹣a+b﹣c>0,
∵c>0,
∴﹣a+b﹣c<c,
∴a﹣b+2c>0,则②正确,
由于无法判定|a﹣b+c|与c的大小,故②错误.
∵﹣ ![]() <﹣
<﹣ ![]() ,
,
∴b>a,
∵x1<﹣1,x2>﹣ ![]() ,
,
∴x1x2<1,
∴ ![]() <1,
<1,
∴a>c,
∴b>a>c,故③正确,
∵b2﹣4ac>0,
∴2ac< ![]() b2 ,
b2 ,
∵b<2a,
∴ ![]() <3ab,
<3ab,
∴ ![]() b2=b2+
b2=b2+ ![]() b2>b2+2ac,
b2>b2+2ac,
b2+2ac< ![]() b2<3ab,
b2<3ab,
∴b2+2ac<3ab.故④正确.
故选C.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】图中是一幅“苹果排列图”,第一行有1个苹果,第二行有2个,第三行有4个,第四行有8个,….你是否发现苹果的排列规律?猜猜看,第十行有_____个苹果;第n行有_____ 个苹果.(可用乘方形式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数-1,2,-3,4,-5,6,…如图排序,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰4”中C的位置是有理数________,有理数“2018”应排在A,B,C,D,E中的________位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是生活中常见的月历表,你对它了解吗?
(1)如果下表是另一个月的月历表,a表示该月中某一天,b,c,d是该月中其他3天,那么b,c,d与a有什么关系?b=________;c=________;d=________(用含a的式子填空).

(2)用一个长方形框圈出月历表中的三个数(如上表中的阴影),若这三个数之和等于51,则这三个数各是多少?
(3)这样圈出的三个数之和可能是64吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,BC⊥CD于点C,∠ABC=30°,∠DEF=45°,则∠CDE等于( )

A. 105° B. 75° C. 135° D. 115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
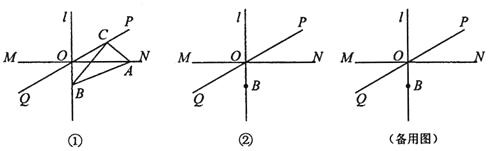
【题目】如图![]() ,直线
,直线![]() ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且![]() 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,![]() 点C在直线PQ上运动
点C在直线PQ上运动![]() 连接BC过点C作
连接BC过点C作![]() ,交直线MN于点A,连接
,交直线MN于点A,连接![]() 点A、C与点O都不重合
点A、C与点O都不重合![]() .
.
![]() 小明经过画图、度量发现:在
小明经过画图、度量发现:在![]() 中,始终有一个角与
中,始终有一个角与![]() 相等,这个角是________________;
相等,这个角是________________;
![]() 当
当![]() 时,在图
时,在图![]() 中画出示意图并证明
中画出示意图并证明![]() ;
;
![]() 探索
探索![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com