
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ________________.
________________.
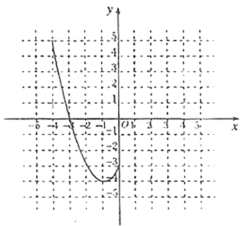
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分;
(3)观察函数图像,写出两条函数的性质;
(4)进一步探究函数图像发现:
①方程![]() 有______个实数根;
有______个实数根;
②函数图像与直线![]() 有_______个交点,所以对应方程
有_______个交点,所以对应方程![]() 有_____个实数根;
有_____个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是___________.
的取值范围是___________.
【答案】(1)-3;(2)见解析;(3)函数![]() 的图象关于y轴对称;当x>1时,y随x的增大而增大;(4)①2;②3,3;③-4<a<-3
的图象关于y轴对称;当x>1时,y随x的增大而增大;(4)①2;②3,3;③-4<a<-3
【解析】
(1)由题意观察表格根据函数的对称性即可求得m的值;
(2)根据题意代入表格数据进行描点、连线即可得到函数的图象;
(3)由题意根据题干所给的函数图象性质进行分析即可;
(4)①根据函数图象与x轴的交点个数,即可得到结论;
②根据![]() 的图象与直线y=-3的交点个数,即可得到结论;
的图象与直线y=-3的交点个数,即可得到结论;
③根据函数的图象即可得到a的取值范围.
解:(1)观察表格根据函数的对称性可得m=-3;
(2)如图所示;
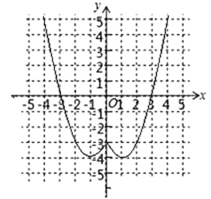
(3)由函数图象知:①函数![]() 的图象关于y轴对称;
的图象关于y轴对称;
②当x>1时,y随x的增大而增大;
(4)①函数图象与x轴有2个交点,所以对应的方程![]() 有2个实数根;
有2个实数根;
②由函数图象知:![]() 的图象与直线y=-3有3个交点,
的图象与直线y=-3有3个交点,
∴方程![]() 有3个实数根;
有3个实数根;
③由函数图象知:∵关于x的方程x2-2![]() -3=a有4个实数根,
-3=a有4个实数根,
∴a的取值范围是-4<a<-3,
故答案为:2,3,3,-4<a<-3.


科目:初中数学 来源: 题型:
【题目】某玩具厂接的600件玩具的订单后,决定由甲、乙两车间共同完成生产任务,已知甲车间工作效率是乙车间的2倍,乙车间单独完成此项生产任务比甲车间单独完成多用10天.
(1)求甲,乙两车间平均每天各能制作多少件玩具;
(2)两车间同时开工3天后,临时又增加了90件的玩具生产任务,为了使完成任务的总时间不超过7天,两车间从第4天起各自提高工作效率,提高工作效率后甲车间工作效率仍是乙车间工作率的2倍,求乙车间提高效率后每天至少生产多少件玩具.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直
,对称轴为直![]() .下列结论:
.下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 若点
若点![]() 点
点![]() 点
点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 对于平面直角坐标系xOy上的点P(a, b) 和抛物线![]() , 我们称P(a, b)是抛物线
, 我们称P(a, b)是抛物线![]() 的相伴点, 抛物线
的相伴点, 抛物线![]() 是点P(a, b) 的相伴抛物线.
是点P(a, b) 的相伴抛物线.
如图,已知点A(-2, -2),B(4, -2),C(1, 4).
(1) 点A的相伴抛物线的解析式为 ;过A, B两点的抛物线![]() 的相伴点坐标为 ;
的相伴点坐标为 ;
(2) 设点P(a, b) 在直线AC上运动:
①点P(a, b)的相伴抛物线的顶点都在同一条抛物线Ω上, 求抛物线Ω的解析式.
②当点P(a, b)的相伴抛物线的顶点落在△ABC 内部时, 请直接写出 a 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年下半年以来,猪肉价格不断上涨,主要是由非洲猪瘟疫情导致.非洲猪瘟疫情发病急,蔓延速度快.某养猪场第一天发现3头生猪发病,两天后发现共有192头生猪发病.
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,按照这样的传染速度,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
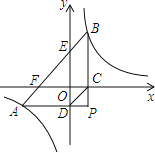
【题目】如图,![]() 的直角顶点P在第四象限,顶点A、B分别落在反比例函数
的直角顶点P在第四象限,顶点A、B分别落在反比例函数![]() 图象的两支上,且
图象的两支上,且![]() 轴于点C,
轴于点C,![]() 轴于点D,AB分别与x轴,y轴相交于点F和
轴于点D,AB分别与x轴,y轴相交于点F和![]() 已知点B的坐标为
已知点B的坐标为![]() .
.
![]() 填空:
填空:![]() ______;
______;
![]() 证明:
证明:![]() ;
;
![]() 当四边形ABCD的面积和
当四边形ABCD的面积和![]() 的面积相等时,求点P的坐标.
的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(2,2),B(﹣1,a)
的图象交于点A(2,2),B(﹣1,a)
(1)求一次函数和反比例函数的表达式;
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点;
①试直接写出当y1>y2时h的取值范围;
②若y1﹣y2=2,试求h的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com