
【题目】已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(2,2),B(﹣1,a)
的图象交于点A(2,2),B(﹣1,a)
(1)求一次函数和反比例函数的表达式;
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点;
①试直接写出当y1>y2时h的取值范围;
②若y1﹣y2=2,试求h的值.
【答案】(1)反比例函数解析式为y2=![]() ,一次函数解析式为y1=2x﹣2;(2)①n>2或﹣1<n<0;②h=1±
,一次函数解析式为y1=2x﹣2;(2)①n>2或﹣1<n<0;②h=1±![]() .
.
【解析】
(1)先把A点坐标代入y2=![]() 求出m得到反比例函数解析式,再通过反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
求出m得到反比例函数解析式,再通过反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)①根据交点坐标结合图象即可求得;
②根据题意得到2h﹣2﹣![]() =2,解方程即可.
=2,解方程即可.
(1)把A(2,2)代入y2=![]() 得m=2×2=4,
得m=2×2=4,
∴反比例函数解析式为y2=![]() ,
,
把B(﹣1,a)代入y=![]() 得a=﹣4,
得a=﹣4,
∴B(﹣1,﹣4),
把A(2,2),B(﹣1,﹣4)代入y1=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y=2x﹣2;
(2)①当y1>y2时h的取值范围为n>2或﹣1<n<0;
②∵点P(h,y1)是一次函数y1=2x﹣2的图象的点,Q(h,y2)是反比例函数y2=![]() 的图象的点,
的图象的点,
∴y1=2h﹣2,y2=![]() ,
,
∵y1﹣y2=2,
∴2h﹣2﹣![]() =2,解得h=1±
=2,解得h=1±![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
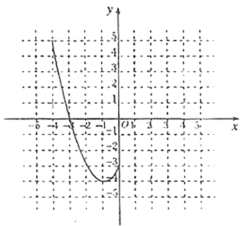
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ________________.
________________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分;
(3)观察函数图像,写出两条函数的性质;
(4)进一步探究函数图像发现:
①方程![]() 有______个实数根;
有______个实数根;
②函数图像与直线![]() 有_______个交点,所以对应方程
有_______个交点,所以对应方程![]() 有_____个实数根;
有_____个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
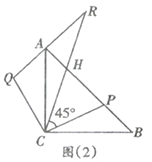
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
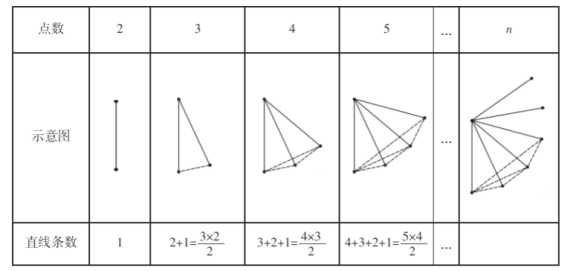
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
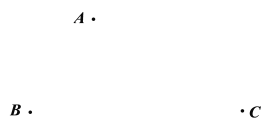
查看答案和解析>>
科目:初中数学 来源: 题型:
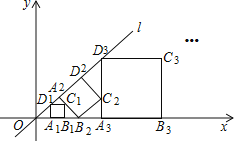
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点A3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形A2019B2019C2019D2019的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
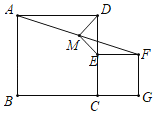
【题目】如图,已知正方形ABCD与正方形CEFG,点E在CD上,点G在BC的延长线上,M是AF的中点,连接DM,EM.
(1)填空:DM与EM数量关系和位置关系为 (直接填写);
(2)若AB=4,设CE=x(0<x<4),△MEF面积为y,求y关于x的函数关系式[可利用(1)的结论],并求出y的最大值;
(3)如果将正方形CEFG绕点C顺时针旋转任意角度,我们发现DM与EM数量关系与位置关系仍未发生改变.
①若正方形ABCD边长AB=13,正方形CEFG边长CE=5,当D,E,F三点旋转至同一条直线上时,求出MF的长;
②证明结论:正方形CEFG绕点C顺时针旋转任意角度,DM与EM数量关系与位置关系仍未发生改变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:在一次聚会上,规定每两个人见面必须握手,且只握手1次.
(1)若参加聚会的人数为3,则共握手___次;若参加聚会的人数为5,则共握手___次;
(2)若参加聚会的人数为![]() (
(![]() 为正整数),则共握手___次;
为正整数),则共握手___次;
(3)若参加聚会的人共握手28次,请求出参加聚会的人数.
拓展:嘉嘉给琪琪出题:“若线段![]() 上共有
上共有![]() 个点(含端点
个点(含端点![]() ,
,![]() ),线段总数为30,求
),线段总数为30,求![]() 的值.”
的值.”
琪琪的思考:“在这个问题上,线段总数不可能为30.”琪琪的思考对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据北京市统计局发布的统计数据显示,北京市近五年国民生产总值数据如图1所示,2017年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示,根据以上信息,下列判断错误的是( )
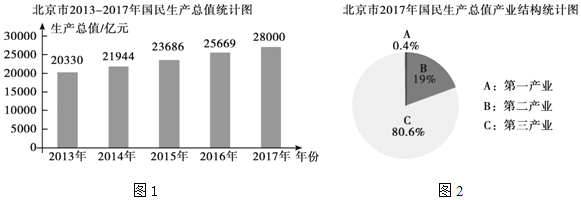
A.2013年至2017年北京市国民生产总值逐年增加
B.2017年第二产业生产总值为5 320亿元
C.2017年比2016年的国民生产总值增加了10%
D.若从2018年开始,每一年的国民生产总值比前一年均增长10%,到2019年的国民生产总值将达到33 880亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com