
【题目】探究:在一次聚会上,规定每两个人见面必须握手,且只握手1次.
(1)若参加聚会的人数为3,则共握手___次;若参加聚会的人数为5,则共握手___次;
(2)若参加聚会的人数为![]() (
(![]() 为正整数),则共握手___次;
为正整数),则共握手___次;
(3)若参加聚会的人共握手28次,请求出参加聚会的人数.
拓展:嘉嘉给琪琪出题:“若线段![]() 上共有
上共有![]() 个点(含端点
个点(含端点![]() ,
,![]() ),线段总数为30,求
),线段总数为30,求![]() 的值.”
的值.”
琪琪的思考:“在这个问题上,线段总数不可能为30.”琪琪的思考对吗?为什么?
【答案】探究:(1)3,10;(2)![]() ;(3)参加聚会的人数为8人;拓展:琪琪的思考对,见解析.
;(3)参加聚会的人数为8人;拓展:琪琪的思考对,见解析.
【解析】
探究:(1)根据握手次数=参会人数×(参会人数-1)÷2,即可求出结论;
(2)由(1)的结论结合参会人数为n,即可得出结论;
(3)由(2)的结论结合共握手28次,即可得出关于n的一元二次方程,解之取其正值即可得出结论;
拓展:将线段数当成握手数,顶点数看成参会人数,由(2)的结论结合线段总数为30,即可得出关于m的一元二次方程,解之由该方程的解均不为整数可得出琪琪的思考对.
探究:(1)3×(3-1)÷2=3,5×(5-1)÷2=10.
故答案为:3;10.
(2)∵参加聚会的人数为n(n为正整数),
∴每人需跟(n-1)人握手,
∴握手总数为![]() .
.
故答案为:![]() .
.
(3)依题意,得:![]() =28,
=28,
整理,得:n2-n-56=0,
解得:n1=8,n2=-7(舍去).
答:参加聚会的人数为8人.
拓展:琪琪的思考对,理由如下:
如果线段数为30,则由题意,得:![]() =30,
=30,
整理,得:m2-m-60=0,
解得m1=![]() ,m2=
,m2=![]() (舍去).
(舍去).
∵m为正整数,
∴没有符合题意的解,
∴线段总数不可能为30.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
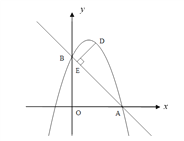
【题目】(满分10分)已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB与这个二次函数的解析式;
(3)在直线AB上方的抛物线上有一动点D,当D与直线AB的距离DE最大时,求点D的坐标,并求DE最大距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
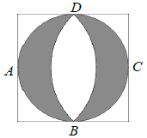
【题目】文艺复兴时期,意大利艺术大师达芬奇曾研究过圆弧所围成的许多图形的面积问题. 如图所示称为达芬奇的“猫眼”,可看成圆与正方形的各边均相切,切点分别为![]() ,
,![]() 所在圆的圆心为点
所在圆的圆心为点![]() (或
(或![]() ). 若正方形的边长为2,则图中阴影部分的面积为( )
). 若正方形的边长为2,则图中阴影部分的面积为( )
A. ![]() B. 2C.
B. 2C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,点B为⊙O上一点,PA切⊙O于点A,PB与AC的延长线交于点M,∠CAB=![]() ∠APB.
∠APB.
(1)求证:PB是⊙O的切线;
(2)当sinM=![]() ,OA=2时,求MB,AB的长.
,OA=2时,求MB,AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com