
分析 首先根据4x2+y2-4x-6y+10=0,可得(2x-1)2+(y-3)2=0,据此求出x、y的值各是多少;然后把求出的x、y的值代入$\frac{2}{3}$x$\sqrt{9x}$-5x$\sqrt{\frac{y}{x}}$,求出算式的值是多少即可.
解答 解:∵4x2+y2-4x-6y+10=0,
∴(2x-1)2+(y-3)2=0,
∴$\left\{\begin{array}{l}{2x-1=0}\\{y-3=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=3}\end{array}\right.$
∴$\frac{2}{3}$x$\sqrt{9x}$-5x$\sqrt{\frac{y}{x}}$
=$\frac{2}{3}×\frac{1}{2}×\sqrt{9×\frac{1}{2}}$-5×$\frac{1}{2}×\sqrt{\frac{3}{\frac{1}{2}}}$
=$\frac{1}{3}×\frac{3\sqrt{2}}{2}$-$\frac{5}{2}×\sqrt{6}$
=$\frac{\sqrt{2}-5\sqrt{6}}{2}$.
点评 (1)此题主要考查了二次根式的化简和求值,要熟练掌握,解答此题的关键是分别求出x、y的值各是多少.
(2)此题还考查了配方法的应用,要明确配方法的理论依据是公式a2±2ab+b2=(a±b)2.


科目:初中数学 来源: 题型:填空题
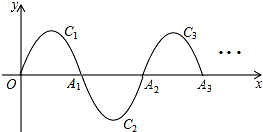 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
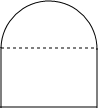 刘师傅是货车司机,他的车高是2.9m、宽2.5m,这次他的运输任务要经过一个如图所示的涵洞.已知半圆拱的圆心距地面2m,半径1.5m,你认为刘师傅能通过这个涵洞吗?
刘师傅是货车司机,他的车高是2.9m、宽2.5m,这次他的运输任务要经过一个如图所示的涵洞.已知半圆拱的圆心距地面2m,半径1.5m,你认为刘师傅能通过这个涵洞吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
| 陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据$\sqrt{21}$≈4.6)
小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据$\sqrt{21}$≈4.6)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com