
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB=![]() ,求BE的长.
,求BE的长.

【答案】(1)见解析;(2)BE=![]()
【解析】
(1)由OB=OC可得∠OBC=∠OCB,由EB=EF可知∠EBC=∠EFB,根据∠AFC+∠OCB=90°可知∠EBC+∠OBC=90°,即可得结论;
(2)由(1)可知∠AEB+∠EAB=90°,由∠AOD+∠EAB=90°即可证明∠AOD=∠AEB,设⊙O的半径为r,根据cos∠AOD=cos∠AEB=![]() 可求出r的值,即可得AB的值,根据cos∠AEB=
可求出r的值,即可得AB的值,根据cos∠AEB=![]() =
=![]() 可得AE=
可得AE=![]() BE,利用勾股定理求出BE的长即可.
BE,利用勾股定理求出BE的长即可.
(1)∵B、C在⊙O上,
∴OB=OC,
∴∠OBC=∠OCB,
∵EF=EB,
∴∠EBC=∠EFB,
又∵∠AFC=∠EFB,
∴∠AFC=∠EBC,
∵AE⊥OC,
∴∠AFC+∠OCB=90°,
∴∠EBC+∠OBC=90°,即BE⊥OB,
又OB是⊙O的半径,
∴EB是⊙O的切线;
(2)设⊙O的半径为r,则OA=OC=r,
又CD=1,
∴OD=r﹣1,
∵∠AOD+∠EAB=90°,∠AEB+∠EAB=90°,
∴∠AOD=∠AEB,
∴cos∠AOD=cos∠AEB=![]() ,
,
∴在Rt△AOD中,cos∠AOD=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:r=![]() ,
,
∵AB是⊙O的直径,
∴AB=5,
在Rt△AEB中,cos∠AEB=![]() =
=![]() ,
,
∴AE=![]() BE,
BE,
又AE2=AB2+BE2,即(![]() BE)2=BE2+52,
BE)2=BE2+52,
解得:BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是___________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中,恰好四个顶点都在横格线上,已知a=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
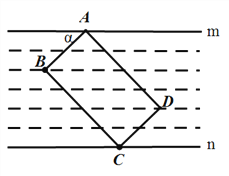
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
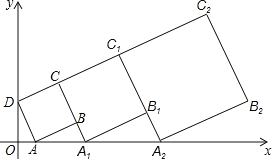
A.5(![]() )2010 B.5(
)2010 B.5(![]() )2010 C.5(
)2010 C.5(![]() )2011 D.5(
)2011 D.5(![]() )2011
)2011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租用4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
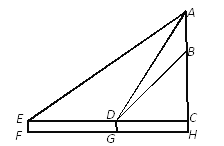
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
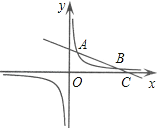
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
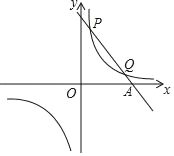
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)写出点P关于原点的对称点P′的坐标;
(2)分别求出这两个函数的表达式;
(3)求∠P′AO的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com