Question

已知关于x的一元二次方程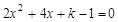有实数根，k为正整数.

（Ⅰ）求k的值；

（Ⅱ）当此方程有两个非零的整数根时，将关于x的二次函数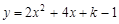的图象向下平移8个单位长度，求平移后的图象的解析式；

（Ⅲ）在（Ⅱ）的条件下，将平移后的二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线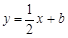（b＜k）与此图象有两个公共点时，b的取值范围．

 

Answer 1

【答案】

（Ⅰ）解：由题意得△=16－8（k－1）=24－8k≥0，∴k≤3.  

 又∵k为正整数，∴k=1，2，3.      

（Ⅱ）当k=1时，方程有一个根为零；  

当k=2时，方程无整数根；     

      当k=3时，方程有两个非零的整数根.

 综上所述，k=1和k=2不合题意，舍去. k=3符合题意.

当k=3时，二次函数为.

把二次函数的图象向下平移8个单位长度得到的

图象解析式为 .           

（Ⅲ）设二次函数的图象与x轴交于A，B两点，则A（－3，0），B（1，0）.

       由题意翻折后的图象如图.

        

     当直线经过点A（－3，0）时，b=.

     当直线经过点B（1，0）时，b=.

     由图象可知，符合题意的b（b＜3）的取值范围为＜b＜

【解析】（I）综合根的判别式及k的要求求出k的取值；

（II）对k的取值进行一一验证，求出符合要求的k值，再结合抛物线平移的规律写出其平移后的解析式；

（III）求出新抛物线与x轴的交点坐标，再分别求出直线y=x+b经过点A、B时的b的取值，进而求出其取值范围．本题第二问是难点，主要是不会借助计算淘汰不合题意的k值．