
【题目】如图,抛物线y=ax2+5ax+c(a<0)与x轴负半轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是抛物线的顶点,过D作DH⊥x轴于点H,延长DH交AC于点E,且S△ABD:S△ACB=9:16,
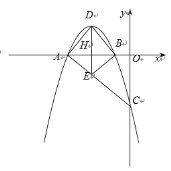
(1)求A、B两点的坐标;
(2)若△DBH与△BEH相似,试求抛物线的解析式.
【答案】(1) ![]() ;(2) 见解析.
;(2) 见解析.
【解析】
(1) 根据顶点公式求出D坐标(利用a,b,c表示),得到OC,DH(利用a,b,c表示)值,因为S△ABD:S△ACB=9:16,所以得到DH:OC=9:16,得到c=4a,利用交点式得出A,B即可.
(2) 由题意可以得到![]() ,求出DH,EH(利用a表示),因为 △DBH与△BEH相似,得到
,求出DH,EH(利用a表示),因为 △DBH与△BEH相似,得到![]() ,即可求出a(注意舍弃正值),得到解析式.
,即可求出a(注意舍弃正值),得到解析式.
解:(1)![]() ∴
∴![]()
∵C(0,c) ∴OC=-c,DH=![]() ∵S△ABD:S△ACB=9∶16
∵S△ABD:S△ACB=9∶16
∴![]() ∴
∴![]()
∴![]() ∴
∴ ![]()
(2)① ∵EH∥OC ∴△AEH∽△ACO ∴![]()
∴![]() ∴
∴ ![]()
∵![]() ∵△DBH与△BEH相似
∵△DBH与△BEH相似
∴∠BDH=∠EBH, 又∵∠BHD=∠BHE=90°∴△DBH∽△BEH
∴![]() ∴
∴![]()
∴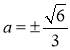 (舍去正值)
(舍去正值)
∴![]()


科目:初中数学 来源: 题型:
【题目】一次函数![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .顶点为
.顶点为![]() 的抛物线经过点
的抛物线经过点![]() .
.
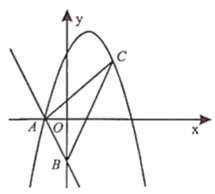
(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一动点.设点
为第一象限抛物线上一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 为何值时,
为何值时,![]() 的值最大,并求
的值最大,并求![]() 的最大值;
的最大值;
(3)在(2)的结论下,若点![]() 在
在![]() 轴上,
轴上,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ABC=90°,AB=BC=2,现将Rt△ABC绕点A逆时针旋转30°得到△AED,则图中阴影部分的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
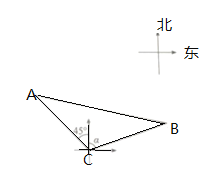
【题目】如图,从灯塔![]() 处观测轮船
处观测轮船![]() 的位置,测得轮船
的位置,测得轮船![]() 在灯塔
在灯塔![]() 北偏西
北偏西![]() 的方向,轮船
的方向,轮船![]() 在灯塔
在灯塔![]() 北偏东
北偏东![]() 的方向,且
的方向,且![]() 海里,
海里,![]() 海里,已知
海里,已知![]() ,求
,求![]() 、
、![]() 两艘轮船之间的距离.(结果保留根号)
两艘轮船之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
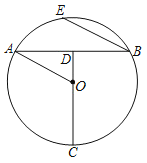
【题目】如图,已知AB是⊙O的弦,点C在⊙O上,且![]() ,联结AO,CO,并延长CO交弦AB于点D,AB=4
,联结AO,CO,并延长CO交弦AB于点D,AB=4![]() ,CD=6.
,CD=6.
(1)求∠OAB的大小;
(2)若点E在⊙O上,BE∥AO,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
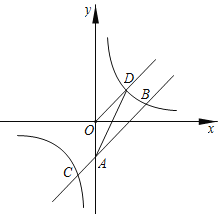
【题目】如图,直线y=x﹣2(k≠0)与y轴交于点A,与双曲线y=![]() 在第一象限内交于点B(3,b),在第三象限内交于点C.
在第一象限内交于点B(3,b),在第三象限内交于点C.
(1)求双曲线的解析式;
(2)直接写出不等式x﹣2>![]() 的解集;
的解集;
(3)若OD∥AB,在第一象限交双曲线于点D,连接AD,求S△AOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com