
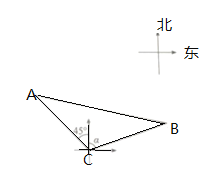
【题目】如图,从灯塔![]() 处观测轮船
处观测轮船![]() 的位置,测得轮船
的位置,测得轮船![]() 在灯塔
在灯塔![]() 北偏西
北偏西![]() 的方向,轮船
的方向,轮船![]() 在灯塔
在灯塔![]() 北偏东
北偏东![]() 的方向,且
的方向,且![]() 海里,
海里,![]() 海里,已知
海里,已知![]() ,求
,求![]() 、
、![]() 两艘轮船之间的距离.(结果保留根号)
两艘轮船之间的距离.(结果保留根号)
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
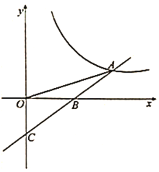
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
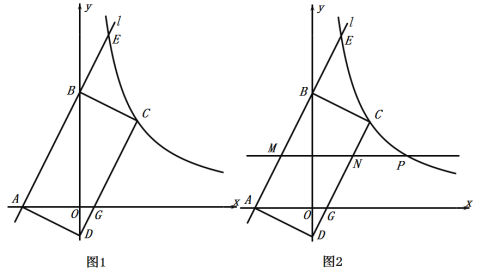
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点A(-1,0)、B(3,0),顶点为C,则下列说法正确的个数是( )
①当-1<x<3时,ax2+bx+c>0;②当△ABC是直角三角形,则a=-![]() ;
;
③若m≤x≤m+3时,二次函数y=ax2+bx+c的最大值为am2+bm+c,则m≥3.
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+5ax+c(a<0)与x轴负半轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是抛物线的顶点,过D作DH⊥x轴于点H,延长DH交AC于点E,且S△ABD:S△ACB=9:16,
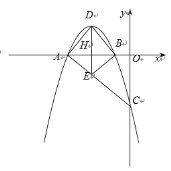
(1)求A、B两点的坐标;
(2)若△DBH与△BEH相似,试求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
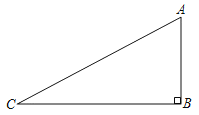
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4,点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.

(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像如图所示,它的对称轴为直线
的图像如图所示,它的对称轴为直线![]() ,与
,与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() ,
,![]() ,且
,且![]() .下列结论中:①
.下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根;⑤
有两个相等的实数根;⑤![]() .其中正确的有( )
.其中正确的有( )
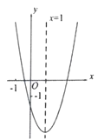
A.②③⑤B.②③C.②④D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①![]() ,②
,②![]() ,③
,③![]() ,④CE2=CDBC.
,④CE2=CDBC.
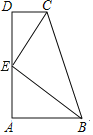
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com