
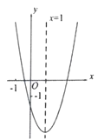
【题目】二次函数![]() 的图像如图所示,它的对称轴为直线
的图像如图所示,它的对称轴为直线![]() ,与
,与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() ,
,![]() ,且
,且![]() .下列结论中:①
.下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根;⑤
有两个相等的实数根;⑤![]() .其中正确的有( )
.其中正确的有( )
A.②③⑤B.②③C.②④D.①④⑤
【答案】A
【解析】
利用抛物线开口方向得到a<0,利用对称轴位置得到b>0,利用抛物线与y轴的交点在x轴下方得c<0,则可对①进行判断;根据二次函数的对称性对②③进行判断;利用抛物线与直线y=2的交点个数对④进行判断,利用函数与坐标轴的交点列出不等式即可判断⑤.
∵抛物线开口向下,
∴a<0,
∵对称轴为直线![]()
∴b=-2a>0
∵抛物线与y轴的交点在x轴下方,
∴c<-1,
∴abc>0,所以①错误;
∵![]() ,对称轴为直线
,对称轴为直线![]()
∴![]() 故
故![]() ,②正确;
,②正确;
∵对称轴x=1,∴当x=0,x=2时,y值相等,
故当x=0时,y=c<0,
∴当x=2时,y=![]() ,③正确;
,③正确;
如图,作y=2,与二次函数有两个交点,
故方程![]() 有两个不相等的实数根,故④错误;
有两个不相等的实数根,故④错误;
∵当x=-1时,y=a-b+c=3a+c>0,
当x=0时,y=c<-1
∴3a>1,
故![]() ,⑤正确;
,⑤正确;
故选A.



 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线![]() (b为常数)的对称轴是直线x=1.
(b为常数)的对称轴是直线x=1.
(1)求该抛物线的表达式;
(2)点A(8,m)在该抛物线上,它关于该抛物线对称轴对称的点为A',求点A'的坐标;
(3)选取适当的数据填入下表,并在如图5所示的平面直角坐标系内描点,画出该抛物线.

查看答案和解析>>
科目:初中数学 来源: 题型:
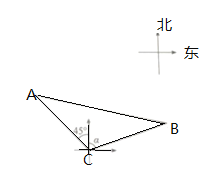
【题目】如图,从灯塔![]() 处观测轮船
处观测轮船![]() 的位置,测得轮船
的位置,测得轮船![]() 在灯塔
在灯塔![]() 北偏西
北偏西![]() 的方向,轮船
的方向,轮船![]() 在灯塔
在灯塔![]() 北偏东
北偏东![]() 的方向,且
的方向,且![]() 海里,
海里,![]() 海里,已知
海里,已知![]() ,求
,求![]() 、
、![]() 两艘轮船之间的距离.(结果保留根号)
两艘轮船之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
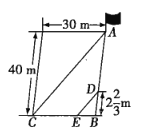
【题目】如图,在一个长40m,宽30m的长方形小操场上,王刚从A点出发,沿着A→B→C的路线以3m/s的速度跑向C地.当他出发4s后,张华有东西需要交给他,就从A地出发沿王刚走的路线追赶,当张华跑到距B地![]() m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
(1)他们的影子重叠时,两人相距多少米(DE的长)?
(2)张华追赶王刚的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点.连接
中点.连接![]() .作
.作![]() ,垂足为
,垂足为![]() ,
,![]() 的外接圆
的外接圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
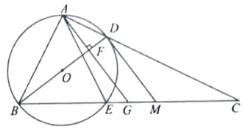
(1)求证:![]() ;
;
(2)过点![]() 作圆
作圆![]() 的切线,交
的切线,交![]() 于点
于点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据全等形的定义,我们把四个角分别相等,四条边分别相等的两个凸四边形叫做全等四边形.
(1)某同学在探究全等四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形全等;( 命题)
②四个角分别相等的两个凸四边形全等;( 命题)
③两个面积相等的正方形全等;( 命题)
④三角分别相等,且其中两角夹边相等两个凸四边形全等.( 命题)
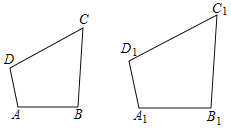
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,AB=A1B1,BC=∠B1C1,CD=C1D1.求证:在四边形ABCD和四边形A1B1C1D1全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(y,﹣x);当x≥0时,点P的变换点P'的坐标为(﹣x,y).
(1)点A(1,2)的变换点A'的坐标是 ;
(2)点B(﹣2,3)的变换点B′在反比例函数y=![]() 的图象上,则k= ,∠BOB'的大小是 °;
的图象上,则k= ,∠BOB'的大小是 °;
(3)点P在抛物线y=﹣(x﹣2n)2+3上,点P的变换P′的坐标是(﹣4,﹣n),求n的值.
(4)点P在抛物线y=﹣x2﹣4x+1的图象上,以线段PP′为对角线作正方形PMP'N,设点P的横坐标为m,当正方形PMP′N的对角线垂直于x轴时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com