
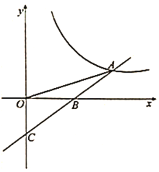
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
【答案】(l)![]() ,
,![]() ;(2)
;(2)![]() 、
、![]() ,
,![]() ,
,![]()
【解析】
(1)根据![]() 可计算出A点的纵坐标,进而利用勾股定理计算出A点的横坐标,代入可得一次函数和反比例函数的解析式.
可计算出A点的纵坐标,进而利用勾股定理计算出A点的横坐标,代入可得一次函数和反比例函数的解析式.
(2)根据题意可得有三种情况,一种是AB为底,一种是AB为腰,以A为顶点,一种是AB为腰,以B为顶点.
(l)过点![]() 作
作![]() 轴于点
轴于点![]()
∵![]()
∴![]()
∴![]()
∵![]() ∴
∴![]()
在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∵![]() 经过点
经过点![]() ∴
∴![]() ∴
∴![]()
∴反比例函数表达式为![]()
∵![]() 经过点
经过点![]() ,点
,点![]()
∴![]() 解得
解得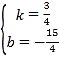
∴一次函数表达式为![]()

(2)本题分三种情况
①当以![]() 为腰,且点
为腰,且点![]() 为顶角顶点时,可得点
为顶角顶点时,可得点![]() 的坐标为
的坐标为![]() 、
、![]()
②当以![]() 为腰,且以点
为腰,且以点![]() 为顶角顶点时,点
为顶角顶点时,点![]() 关于
关于![]() 的对称点即为所求的点
的对称点即为所求的点![]()
③当以![]() 为底时,作线段
为底时,作线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,则点
,则点![]() 即为所求
即为所求
由(1)得,![]()
在![]() 中,
中,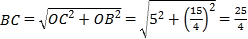
∵![]()
∴![]() ∴
∴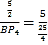 ∴
∴![]() ∴
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
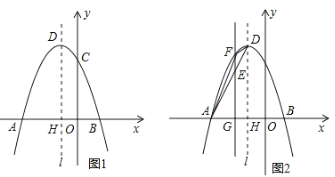
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,E,F分别是边AB,CD的中点,M,N分别是边AD,AB上两点,将△AMN沿MN对折,使点A落在点E上.若AB=a,BC=b,且N是FB的中点,则![]() 的值为____.
的值为____.
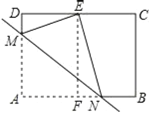
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,连结AC,分别交DE,DF于点M,N.
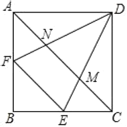
(1)求证:△ADF≌△CDE;
(2)设△DMN和△AFN的面积分别为S1和S2;
①若∠ADF=∠EDF,求S2:S1的值.
②若S2=2S1,求tan∠ADF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
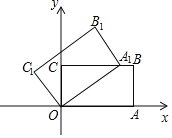
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
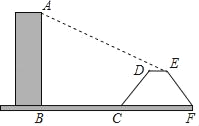
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进生态文明建设,加快发展新能源汽车,国家对新能源汽车实行补贴政策。一家4S店从事某品牌纯电动汽车和插电式混动汽车两种新能源汽车(以下简称电动车和混动车)的销售,电动车每辆进价16万元,去年国家对该车每辆补贴4.5万元,补贴后每辆售价14万元;混动车每辆进价18万元,去年国家对该车每辆补贴2.8万元,补贴后每辆售价18万元。该4S店去年12月共销售这两种汽车120辆,获得利润324万元。
(1)求该4S店去年12月销售了多少辆混动车?
(2)今年国家对该品牌新能源汽车的补贴有所下降,电动车每辆比去年少补贴0.5万元,混动车每辆比去年少补贴0.8万元,该4S店为减少损失,今年1月把电动车的售价提高了m%,结果销量在去年12月的基础上减少了![]() m%,对混动车的售价没有作调整,而销量在去年12月的基础上增加了2.4m辆,结果该4S店今年1月的利润比去年12月少了14万元,求m的值。
m%,对混动车的售价没有作调整,而销量在去年12月的基础上增加了2.4m辆,结果该4S店今年1月的利润比去年12月少了14万元,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD是⊙O的两条互相垂直的直径,E是![]() 上一点,连接AE,作OG∥AE交CE于点G.
上一点,连接AE,作OG∥AE交CE于点G.
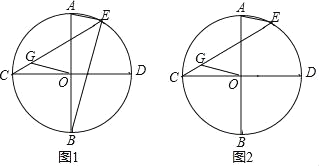
(1)求证:BE=![]() EG;
EG;
(2)判断AE与CG的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com