
【题目】如图,AB、CD是⊙O的两条互相垂直的直径,E是![]() 上一点,连接AE,作OG∥AE交CE于点G.
上一点,连接AE,作OG∥AE交CE于点G.
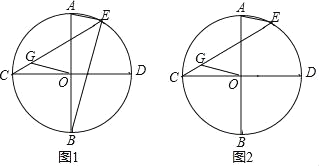
(1)求证:BE=![]() EG;
EG;
(2)判断AE与CG的数量关系,并证明.
【答案】(1)证明见解析;
(2)![]() .
.
【解析】
作OH⊥OG,交CE于H,连接AH,先证明△COG≌△AOH(SAS),可得出CG=AH和∠AHO=∠CGO=135°,得出![]() ,再由AB、CD是⊙O的两条互相垂直的直径得出
,再由AB、CD是⊙O的两条互相垂直的直径得出![]() ,进而证的△BCG∽△BAE,得出∠CEB=45°,从而证的△BGE三等腰直角三角形,即可得出BE=
,进而证的△BCG∽△BAE,得出∠CEB=45°,从而证的△BGE三等腰直角三角形,即可得出BE=![]() EG.
EG.
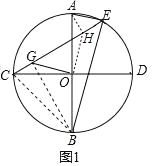
(1)如图1,证明:作OH⊥OG,交CE于H,连接AH,
∵OG∥AE,
∴∠OGH=∠AEC=45°,
∴∠OHG=45°,
∴OG=OH,
又∵∠COG=∠AOH=90°﹣∠AOG,OC=OA,
∴△COG≌△AOH(SAS),
∴CG=AH,∠AHO=∠CGO=135°,
∴∠AHC=90°,
∴AE=![]() AH=
AH=![]() CG,
CG,
∴![]() ,
,
∵AB、CD是⊙O的两条互相垂直的直径,
∴OC=OB=![]() AB,
AB,
连接BC,BG,
∴![]() ,
,
∴![]() ,
,
∵∠BCG=∠BAE,
∴△BCG∽△BAE,
∴∠CGB=∠AEB=90°,
∵∠CEB=45°,
∴△BGE三等腰直角三角形,
∴BE=![]() EG;
EG;
(2)解:作OH⊥OG,交CE于H,连接AH,
∵OG∥AE,
∴∠OGH=∠AEC=45°,
∴∠OHG=45°,
∴OG=OH,
又∵∠COG=∠AOH=90°﹣∠AOG,OC=OA,
∴△COG≌△AOH(SAS),
∴CG=AH,∠AHO=∠CGO=135°,
∴∠AHC=90°,
∴AE=![]() AH=
AH=![]() CG,
CG,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
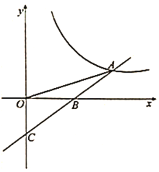
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校国”的目标,兴义市某学校开展了多场足球比赛在某场比赛中,一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果要求足球的最大高度达到20m,那么足球被踢出时的速度应该达到( )
A. 5m/s B. 10m/s C. 20m/s D. 40m/s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数y1=x2+kx+k﹣1(k为常数)
(1)对任意实数k,函数图象与x轴都有交点
(2)若当x≥75时,函数y的值都随x的增大而增大,求满足条件的最小整数k的值
(3)K取不同的值时,函数抛物线的顶点位置也会变化,但会在某一函数图象上,求该函数图象的解析式
(4)若当自变量x满足0≤x≤3时,与其对应的函数值y的最小值为10,求此时k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
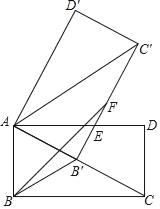
【题目】如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.
(1)求证:AE=C′E.
(2)求∠FBB'的度数.
(3)已知AB=2,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com