
【题目】关于x的二次函数y1=x2+kx+k﹣1(k为常数)
(1)对任意实数k,函数图象与x轴都有交点
(2)若当x≥75时,函数y的值都随x的增大而增大,求满足条件的最小整数k的值
(3)K取不同的值时,函数抛物线的顶点位置也会变化,但会在某一函数图象上,求该函数图象的解析式
(4)若当自变量x满足0≤x≤3时,与其对应的函数值y的最小值为10,求此时k的值.
【答案】(1)见解析;(2)﹣150;(3)y=﹣x2﹣2x﹣1;(4)11.
【解析】
(1)计算△,根据△的值进行判断;
(2)根据二次函数的增减性即可判断;
(3)得到抛物线的顶点,写成方程组,消去k得y=-x2-2x-1,即可判断;
(4)函数配方后得y=x2+kx+k-1= ,根据对称轴的位置分三种情况进行讨论可得结论.
,根据对称轴的位置分三种情况进行讨论可得结论.
解:(1)∵△=k2﹣4(k﹣1)=k2﹣4k+4=(k﹣2)2≥0,
∴对任意实数k,函数图象与x轴都有交点;
(2)∵a=1>0,抛物线的对称轴x![]() ,
,
∴在对称轴的右侧函数y的值都随x的增大而增大,
即当x![]() 时,函数y的值都随x的增大而增大,
时,函数y的值都随x的增大而增大,
∵x≥75时,函数y的值都随x的增大而增大,
∴![]() 75,k≥﹣150,
75,k≥﹣150,
∴k的最小整数是﹣150,
∴满足条件的最小整数k的值是﹣150;
(3)∵y=x2+kx+k﹣1=(x![]() )2
)2![]() k﹣1,
k﹣1,
∴抛物线的顶点为(![]() ,
,![]() k﹣1),
k﹣1),
∴ ,
,
消去k得,y=﹣x2﹣2x﹣1,
由此可见,不论k取任何实数,抛物线的顶点都满足函数y=﹣x2﹣2x﹣1,
即抛物线的顶点在二次函数y=﹣x2﹣2x﹣1的图象上;
(4)∵y=x2+kx+k﹣1=(x![]() )2
)2![]() k﹣1,
k﹣1,
∴抛物线的顶点为(![]() ,
,![]() k﹣1),
k﹣1),
又∵0≤x≤3时,与其对应的函数值y的最小值为10,
①当![]() 0时,即k≤0,
0时,即k≤0,
此时x=0时,y取得最小值是10,
则有10=k﹣1,
k=11.
②当![]() 3时,即k≤﹣6,
3时,即k≤﹣6,
此时x=3时,y取得最小值是10,
则有10=32+3k+k﹣1,
k![]() ,不符合题意;
,不符合题意;
③当0![]() 3时,即﹣6<k<0,
3时,即﹣6<k<0,
此时x![]() 时,y取得最小值是10,
时,y取得最小值是10,
即![]() k﹣1=10,
k﹣1=10,
此方程无实根,
综上所述,k的值是11.


科目:初中数学 来源: 题型:
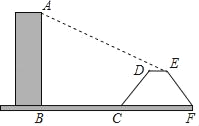
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调查价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.
(1)直接写出每周售出商品的利润y(单位:元)与每件降价x(单位:元)之间的函数关系式,直接写出自变量x的取值范围;
(2)涨价多少元时,每周售出商品的利润为2250元;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD是⊙O的两条互相垂直的直径,E是![]() 上一点,连接AE,作OG∥AE交CE于点G.
上一点,连接AE,作OG∥AE交CE于点G.
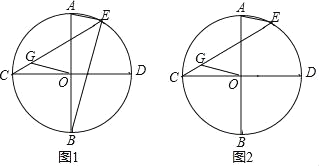
(1)求证:BE=![]() EG;
EG;
(2)判断AE与CG的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小禾和小野按图示的规则玩“锤子”“剪刀”“布”游戏,游戏规则为:若一人出“剪刀”另一个出“布”,则出“剪刀”的胜;若一人出“锤子”另一个出“剪刀”,则出“锤子”的胜;若一人出“布”另一个出“锤子”,则出“布”的胜.若两人出相同的手势,则两人平局.
(1)用树状图或者表格表示小禾和小野玩一次所有可能的结果.

(2)这个游戏玩一次,小禾和小野分别胜出的概率是多少?从而说明游戏的公平性?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP=( )

A.6或4.5B.6C.3D.4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=![]() ,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点
,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点
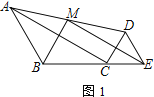
(1)如图1,当B、C、E三点共线时,证明: BM⊥ME
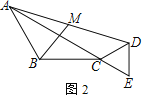
(2)如图2,当A、C、E三点共线时,求BM的长
(3)如图3,取BE中点N,连MN.将△CDE绕点C旋转,直接写出旋转过程中线段MN的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
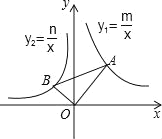
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )
A.m=![]() nB.m=﹣
nB.m=﹣![]() nC.m=﹣
nC.m=﹣![]() nD.m=﹣3n
nD.m=﹣3n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com