
【题目】如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,连结AC,分别交DE,DF于点M,N.
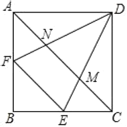
(1)求证:△ADF≌△CDE;
(2)设△DMN和△AFN的面积分别为S1和S2;
①若∠ADF=∠EDF,求S2:S1的值.
②若S2=2S1,求tan∠ADF.
【答案】(1)见解析;(2)①S2:S1的值为![]() ;②tan∠ADF=
;②tan∠ADF=![]() ﹣1.
﹣1.
【解析】
(1)根据HL证明三角形全等即可;
(2)①如图,作NH⊥AB于H.设FH=a.利用参数表示S2,S1即可;
②如图,作NH⊥AB于H.易证∠ADF=∠HNF,设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,利用面积关系构建方程求出k即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAF=∠DCE=∠ADC=90°,
∵DF=DE,
∴Rt△ADF≌Rt△CDE(HL).
(2)①如图,作NH⊥AB于H.设FH=a.

∵Rt△ADF≌Rt△CDE(HL),
∵∠ADF=∠CDE,
∵∠ADF=∠DEF,
∴∠ADF=∠EDF=∠CDE=30°,
∴∠AFD=60°,
∵∠NHF=90°,
∴∠FNH=30°,
∴HN=![]() a,
a,
∵∠NAH=45°,∠AHN=90°,
∴∠NAH=∠ANH=45°,
∴HA=HN=![]() a,
a,
∴AF=(1+![]() )a,AD=
)a,AD=![]() AF=(3+
AF=(3+![]() )a,
)a,
∴S2=![]() AFNH=
AFNH=![]() (1+
(1+![]() )a
)a![]() a=
a=![]() a2,
a2,
∵∠ADN=∠CDM,AD=DC,∠DAN=∠DCM=45°,
∴△ADN≌△CDM(ASA),
∴S△ADN=S△DCM,
∴S1=S△ADC﹣2S△ADN=![]() [(3+
[(3+![]() )a]2﹣2×
)a]2﹣2×![]() (3+
(3+![]() )a
)a![]() a=(9+6
a=(9+6![]() )a2,
)a2,
∴ .
.
(3)如图,作NH⊥AB于H.

∵∠FHN=∠FAD=90°,
∴HN∥AD,
∴∠ADF=∠HNF,
设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,
∴AF=b+kb,
∴AD=![]() ,
,
∴S2=![]() [(1+k)b]2,S1=S△ADC﹣2S△ADN=
[(1+k)b]2,S1=S△ADC﹣2S△ADN=![]() ﹣2×
﹣2×![]() ,
,
∵S2=2S1,
∴![]() (1+k)b]2=2[
(1+k)b]2=2[![]() ﹣2×
﹣2×![]() ]
]
整理得:k2+2k﹣2=0,
解得:k=![]() ﹣1或
﹣1或![]() ﹣1(舍弃),
﹣1(舍弃),
∴tan∠ADF=k=![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t=±9因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上),若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α度(0<α<180),当边DE与△ABC的某一边平行时,相应的旋转角α的值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
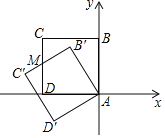
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
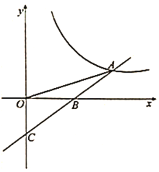
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校国”的目标,兴义市某学校开展了多场足球比赛在某场比赛中,一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果要求足球的最大高度达到20m,那么足球被踢出时的速度应该达到( )
A. 5m/s B. 10m/s C. 20m/s D. 40m/s
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com