
【题目】如图,正方形ABCD的边长为6,点E、F分别在AB、AD上,若CE=3![]() ,且∠ECF=45°,则AF的长为( )
,且∠ECF=45°,则AF的长为( )
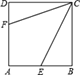
A.4B.3C.2.5D.2
【答案】A
【解析】
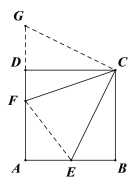
延长FD到G,使DG=BE,连接CG、EF,先利用正方形的性质和SAS证明△BCE≌△DCG,得CE=CG,再利用SAS证明△GCF≌△ECF,于是GF=EF,然后利用勾股定理求出BE的长,设AF=x,在Rt△AEF中利用勾股定理列出方程,解方程即得答案.
解:如图,延长FD到G,使DG=BE,连接CG、EF;
∵四边形ABCD为正方形,∴BC=DC,∠B=∠CDG=90°,
∴△BCE≌△DCG(SAS),
∴CE=CG,∠BCE=∠DCG,
∵∠BCE+∠DCF=45°,∴∠DCG+∠DCF=45°,∴∠GCF=45°,
∴∠GCF=∠ECF,又∵CF=CF,∴△GCF≌△ECF(SAS),∴GF=EF,
∵CE=3![]() ,CB=6,∴BE=
,CB=6,∴BE=![]() =3,∴AE=3,
=3,∴AE=3,
设AF=x,则DF=6﹣x,GF=3+(6﹣x)=9﹣x,∴EF=9﹣x.
在Rt△AEF中,由勾股定理得:(9﹣x)2=9+x2,
解得:x=4,即AF=4.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
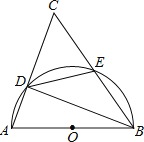
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,连结AC,分别交DE,DF于点M,N.
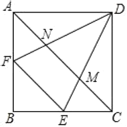
(1)求证:△ADF≌△CDE;
(2)设△DMN和△AFN的面积分别为S1和S2;
①若∠ADF=∠EDF,求S2:S1的值.
②若S2=2S1,求tan∠ADF.
查看答案和解析>>
科目:初中数学 来源: 题型:
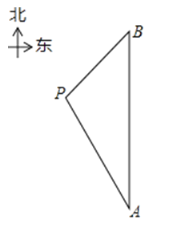
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
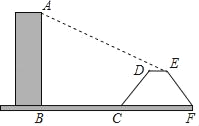
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
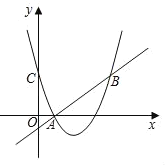
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,把长与宽之比为![]() (或宽与长之比为
(或宽与长之比为![]() )的矩形称为黄金矩形.
)的矩形称为黄金矩形.
思考解决下列问题:
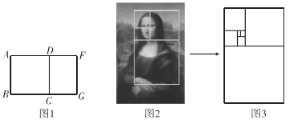
(1)已知图1中黄金矩形![]() 的长
的长![]() ,求
,求![]() 的长;
的长;
(2)黄金矩形有个奇妙的特性:把图1中的黄金矩形![]() ,以
,以![]() 为边向矩形内作正方形
为边向矩形内作正方形![]() ,则矩形
,则矩形![]() 是否为黄金矩形,是,请予以证明;不是,请说明理由;
是否为黄金矩形,是,请予以证明;不是,请说明理由;
(3)黄金矩形使名画《蒙娜丽莎》显得特别和谐,专家分析画中布局如图2,其中最外面的矩形是黄金矩形,以黄金矩形的宽为边向矩形内部作正方形,由上小题知产生的小矩形为更小的黄金矩形,按此规律依次生成各黄金矩形,若图3中最大黄金矩形的长为![]() ,则最小黄金矩形的长是多少?
,则最小黄金矩形的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小禾和小野按图示的规则玩“锤子”“剪刀”“布”游戏,游戏规则为:若一人出“剪刀”另一个出“布”,则出“剪刀”的胜;若一人出“锤子”另一个出“剪刀”,则出“锤子”的胜;若一人出“布”另一个出“锤子”,则出“布”的胜.若两人出相同的手势,则两人平局.
(1)用树状图或者表格表示小禾和小野玩一次所有可能的结果.

(2)这个游戏玩一次,小禾和小野分别胜出的概率是多少?从而说明游戏的公平性?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com