
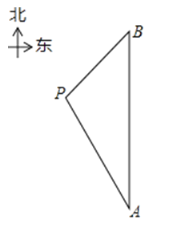
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
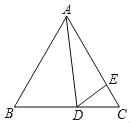
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
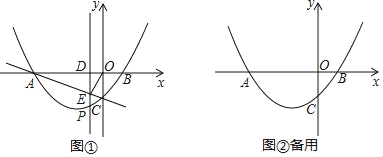
【题目】如图,抛物线y=![]() 与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
(1)点B的坐标为 ,直线AC的关系式为 .
(2)设在直线AC下方的抛物线上有一动点P,过点P作PD⊥x轴于D,交直线AC于点E,当CE平分∠OEP时求点P的坐标.
(3)点M在x轴上,点N在抛物线上,试问以点A、C、M、N为顶点的四边形能否成为平行四边形?若存在,直接写出所有点M的坐标;若不存在,请简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=14x2+1(如图所示).
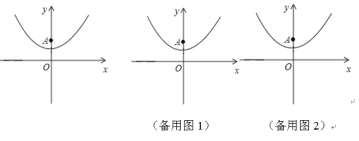
(1)填空:抛物线的顶点坐标是(___,___),对称轴是___;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B. 若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上。在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,
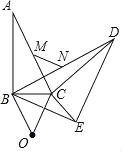
(1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是 (填写序号即可);
(2)判断∠A和∠BEC的数量关系,并证明;
(3)点N是BD的中点,连接MN,若MN=2,求BE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com