
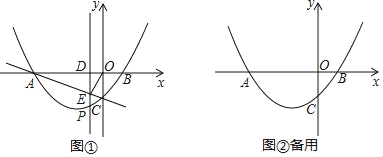
【题目】如图,抛物线y=![]() 与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
(1)点B的坐标为 ,直线AC的关系式为 .
(2)设在直线AC下方的抛物线上有一动点P,过点P作PD⊥x轴于D,交直线AC于点E,当CE平分∠OEP时求点P的坐标.
(3)点M在x轴上,点N在抛物线上,试问以点A、C、M、N为顶点的四边形能否成为平行四边形?若存在,直接写出所有点M的坐标;若不存在,请简述你的理由.
【答案】(1)(2,0),y=![]() x﹣4;(2)P(﹣
x﹣4;(2)P(﹣![]() ,﹣
,﹣![]() );(3)M的坐标为:(5+
);(3)M的坐标为:(5+![]() ,0)或(5﹣
,0)或(5﹣![]() )或(﹣14,0)或(﹣2,0).
)或(﹣14,0)或(﹣2,0).
【解析】
(1)令y=0,解关于x的一元二次方程即可求出点A、B的坐标,令x=0即可求出点C的坐标;根据待定系数法即可求出直线AC的解析式;
(2)先证明OE=OC=4,再设点E的坐标为(m,![]() m﹣4),然后在Rt△ODE中根据勾股定理即可得出关于m的一元二次方程,解方程即可求出m的值,进一步即可求出结果;
m﹣4),然后在Rt△ODE中根据勾股定理即可得出关于m的一元二次方程,解方程即可求出m的值,进一步即可求出结果;
(3)①当AC是平行四边形的边时,根据A到C的平移规律可得N(M)到M(N)的平移规律,解方程即可求得结果;②当AC是平行四边形的对角线时,利用中点坐标公式求解即可.
解:(1)y=![]() ,令y=0,则
,令y=0,则![]() ,解得x=2或﹣8,令x=0,则y=﹣4,
,解得x=2或﹣8,令x=0,则y=﹣4,
所以点A、B、C的坐标分别为:(﹣8,0)、(2,0)、(0,﹣4),
将点A、C的坐标代入一次函数表达式:y=kx+b得:![]() ,解得:
,解得: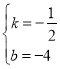 ,
,
故直线AC的表达式为:y=![]() x﹣4;
x﹣4;
故答案为:(2,0),y=![]() x﹣4;
x﹣4;
(2)如图,∵CE平分∠OEP,∴∠OEC=∠CEP,
∵PD∥y轴,∴∠CEP=∠ECO=∠OEC,∴OE=OC=4,
设点E的坐标为(m,![]() m﹣4),
m﹣4),
则在Rt△ODE中,根据勾股定理,得![]() ,
,
解得:m=﹣![]() 或0(不和题意,舍去),
或0(不和题意,舍去),
由于P、E的横坐标相等,所以点P(﹣![]() ,﹣
,﹣![]() );
);
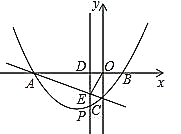
(3)设点M(s,0),N(m,n),则n=![]() m2+
m2+![]() m﹣4,
m﹣4,
①当AC是平行四边形的边时,
则点A向右平移8个单位,再向下平移4个单位得到C,
同理N(M)向右平移8个单位,再向下平移4个单位得到M(N),
即m+8=s,n﹣4=0或m﹣8=s,n+4=0,而n=![]() m2+
m2+![]() m﹣4,
m﹣4,
当m+8=s,n﹣4=0时,4=![]() m2+
m2+![]() m﹣4,解得:
m﹣4,解得:![]() ,所以s=5±
,所以s=5±![]() ;
;
当m﹣8=s,n+4=0时,-4=![]() m2+
m2+![]() m﹣4,解得:m=﹣6或0(舍去),所以s=﹣14;
m﹣4,解得:m=﹣6或0(舍去),所以s=﹣14;
②当AC是平行四边形的对角线时,
利用中点坐标公式得:﹣8=m+s,﹣4=n,而n=![]() m2+
m2+![]() m﹣4,解得:s=﹣2;
m﹣4,解得:s=﹣2;
综上,s=5±![]() 或﹣14或﹣2;
或﹣14或﹣2;
故点M的坐标为:(5+![]() ,0)或(5﹣
,0)或(5﹣![]() )或(﹣14,0)或(﹣2,0).
)或(﹣14,0)或(﹣2,0).


科目:初中数学 来源: 题型:
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
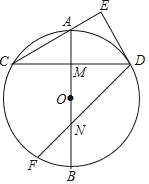
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
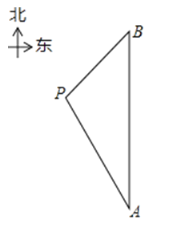
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
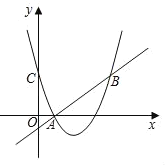
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
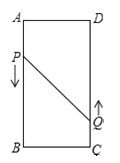
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
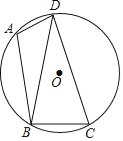
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=100°,∠DBC=80°.
(1)求证:BD=CD;
(2)若圆O的半径为9,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com