
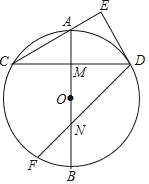
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
【答案】(1)60;(2)证明见解析;(3)![]() .
.
【解析】
(1)由CD⊥AB和M是OA的中点,利用三角函数可以得到∠DOM=60°,进而得到△OAD是等边三角形,∠OAD=60°.
(2)只需证明DE⊥OD.便可以得到DE与⊙O相切.
(3)利用圆的综合知识,可以证明,∠CND=90°,∠CFN=60°,根据特殊角的三角函数值可以得到FN的数值.
解:(1)如图1,连接OD,AD

∵AB是⊙O的直径,CD⊥AB
∴AB垂直平分CD
∵M是OA的中点,
∴OM=![]() OA=
OA=![]() OD
OD
∴cos∠DOM=![]() =
=![]() ,
,
∴∠DOM=60°
又:OA=OD
∴△OAD是等边三角形
∴∠OAD=60°
故答案为:60°
(2)∵CD⊥AB,AB是⊙O的直径,
∴CM=MD.
∵M是OA的中点,
∴AM=MO.
又∵∠AMC=∠DMO,
∴△AMC≌△OMD.
∴∠ACM=∠ODM.
∴CA∥OD.
∵DE⊥CA,
∴∠E=90°.
∴∠ODE=180°﹣∠E=90°.
∴DE⊥OD.
∴DE与⊙O相切.
(3)如图2,连接CF,CN,

∵OA⊥CD于M,
∴M是CD中点.
∴NC=ND.
∵∠CDF=45°,
∴∠NCD=∠NDC=45°.
∴∠CND=90°.
∴∠CNF=90°.
由(1)可知∠AOD=60°.
∴∠ACD=![]() ∠AOD=30°.
∠AOD=30°.
在Rt△CDE中,∠E=90°,∠ECD=30°,DE=3,
∴CD=![]() ,
,
在Rt△CND中,∠CND=90°,∠CDN=45°,CD=6,
∴CN=CD·sin45°=3![]() .
.
由(1)知∠CAD=2∠OAD=120°,
∴∠CFD=180°﹣∠CAD=60°.
在Rt△CNF中,∠CNF=90°,∠CFN=60°,CN=3![]() ,
,
∴FN=![]() .
.


科目:初中数学 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:

根据所给信息,解决下列问题:
(1)a= ,b= ;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:

(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
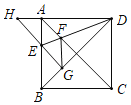
【题目】如图,已知正方形ABCD的边长为1,将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.下列结论中正确的有( )
①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
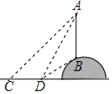
【题目】如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°
(1)求证:AB=BD;
(2)求证铁塔AB的高度.(结果精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1.有下列4个结论:①abc>0;②4a+2b+c>0;③2c<3b;④a+b>m(am+b)(m是不等于1的实数).其中正确的结论个数有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数![]() 和反比例函数
和反比例函数![]() 的图象都经过点(1,1)(1)求反比例函数的解析式.(2)已知点
的图象都经过点(1,1)(1)求反比例函数的解析式.(2)已知点![]() 在第三象限,且同时在两个函数的图像上,求点
在第三象限,且同时在两个函数的图像上,求点![]() 的坐标.(3)利用(2)的结果,若点
的坐标.(3)利用(2)的结果,若点![]() 的坐标为(2,0),且以点
的坐标为(2,0),且以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,请你直接写出点
为顶点的四边形是平行四边形,请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
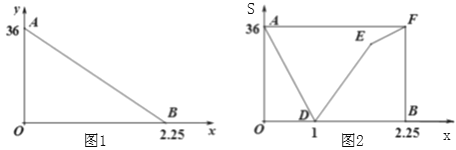
【题目】“低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑车前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离S(km)与出发时间x(h)之间的函数关系式如图2中折线段CD-DE-EF所示.
(1)小丽和小明骑车的速度各是多少?
(2)求E点坐标,并解释点的实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com