
【题目】已知抛物线y=14x2+1(如图所示).
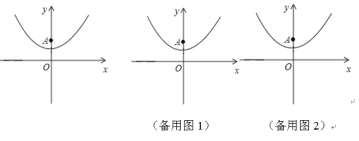
(1)填空:抛物线的顶点坐标是(___,___),对称轴是___;
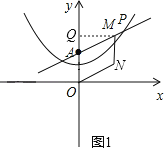
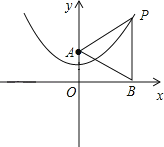
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B. 若△PAB是等边三角形,求点P的坐标;
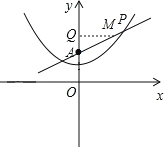
(3)在(2)的条件下,点M在直线AP上。在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由。
【答案】(1)(1)顶点坐标是(0,1),对称轴是y轴(或x=0);(2)P1(2![]() ,4),P2(﹣2
,4),P2(﹣2![]() ,4);(3)存在N1(
,4);(3)存在N1(![]() ,1),N2(﹣
,1),N2(﹣![]() ,﹣1)N3(﹣
,﹣1)N3(﹣![]() ,1),N4(
,1),N4(![]() ,﹣1)使得四边形OAMN是菱形.
,﹣1)使得四边形OAMN是菱形.
【解析】
(1)根据函数的解析式直接写出其顶点坐标和对称轴即可;
(2)根据等边三角形的性质求得PB=4,将PB=4代入函数的解析式后求得x的值即可作为P点的横坐标,代入解析式即可求得P点的纵坐标;
(3)首先求得直线AP的解析式,然后设出点M的坐标,利用勾股定理表示出有关AP的长即可得到有关M点的横坐标的方程,求得M的横坐标后即可求得其纵坐标,
解:(1)顶点坐标是(0,1),对称轴是y轴(或x=0).
(2)∵△PAB是等边三角形,
∴∠ABO=90°﹣60°=30°.
∴AB=20A=4.
∴PB=4.
解法一:把y=4代入y=![]() x2+1,
x2+1,
得 x=±2![]() .
.
∴P1(2![]() ,4),P2(﹣2
,4),P2(﹣2![]() ,4).
,4).
解法二:∴OB=![]() =2
=2![]()
∴P1(2![]() ,4).
,4).
根据抛物线的对称性,得P2(﹣2![]() ,4).
,4).
(3)∵点A的坐标为(0,2),点P的坐标为(2![]() ,4)
,4)
∴设线段AP所在直线的解析式为y=kx+b
∴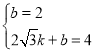
解得: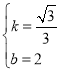
![]() x+2
x+2
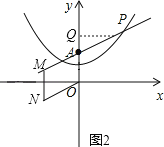
设存在点N使得OAMN是菱形,
∵点M在直线AP上,
∴设点M的坐标为:(m,![]() m+2)
m+2)
如图,作MQ⊥y轴于点Q,则MQ=m,AQ=OQ﹣OA=![]() m+2﹣2=
m+2﹣2=![]() m
m
∵四边形OAMN为菱形,
∴AM=AO=2,
∴在直角三角形AMQ中,AQ2+MQ2=AM2,
即:m2+(![]() m)2=22
m)2=22
解得:m=±![]()
代入直线AP的解析式求得y=3或1,
当P点在抛物线的右支上时,分为两种情况:
当N在右图1位置时,
∵OA=MN,
∴MN=2,
又∵M点坐标为(![]() ,3),
,3),
∴N点坐标为(![]() ,1),即N1坐标为(
,1),即N1坐标为(![]() ,1).
,1).
当N在右图2位置时,
∵MN=OA=2,M点坐标为(﹣![]() ,1),
,1),
∴N点坐标为(﹣![]() ,﹣1),即N2坐标为(﹣
,﹣1),即N2坐标为(﹣![]() ,﹣1).
,﹣1).
当P点在抛物线的左支上时,分为两种情况:
第一种是当点M在线段PA上时(PA内部)我们求出N点坐标为(﹣![]() ,1);
,1);
第二种是当M点在PA的延长线上时(在第一象限)我们求出N点坐标为(![]() ,﹣1)
,﹣1)
∴存在N1(![]() ,1),N2(﹣
,1),N2(﹣![]() ,﹣1)N3(﹣
,﹣1)N3(﹣![]() ,1),N4(
,1),N4(![]() ,﹣1)使得四边形OAMN是菱形.
,﹣1)使得四边形OAMN是菱形.


科目:初中数学 来源: 题型:
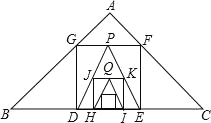
【题目】如图,已知在Rt△ABC中,AB=AC=3![]() ,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
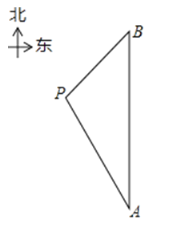
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
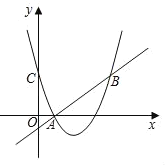
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,把长与宽之比为![]() (或宽与长之比为
(或宽与长之比为![]() )的矩形称为黄金矩形.
)的矩形称为黄金矩形.
思考解决下列问题:
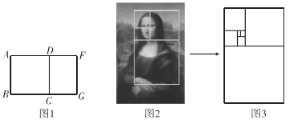
(1)已知图1中黄金矩形![]() 的长
的长![]() ,求
,求![]() 的长;
的长;
(2)黄金矩形有个奇妙的特性:把图1中的黄金矩形![]() ,以
,以![]() 为边向矩形内作正方形
为边向矩形内作正方形![]() ,则矩形
,则矩形![]() 是否为黄金矩形,是,请予以证明;不是,请说明理由;
是否为黄金矩形,是,请予以证明;不是,请说明理由;
(3)黄金矩形使名画《蒙娜丽莎》显得特别和谐,专家分析画中布局如图2,其中最外面的矩形是黄金矩形,以黄金矩形的宽为边向矩形内部作正方形,由上小题知产生的小矩形为更小的黄金矩形,按此规律依次生成各黄金矩形,若图3中最大黄金矩形的长为![]() ,则最小黄金矩形的长是多少?
,则最小黄金矩形的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
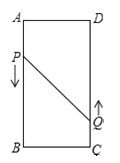
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线解析式可以是![]() 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a= ;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是 ;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线![]() 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com