
【题目】我们知道,经过原点的抛物线解析式可以是![]() 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a= ;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是 ;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线![]() 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
【答案】(1)-1;![]() (2)
(2)![]() (3)3,6,9
(3)3,6,9
【解析】
解:(1)-1;![]() 。
。
(2)∵过原点的抛物线顶点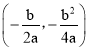 在直线
在直线![]() 上,∴
上,∴![]() 。
。
∵b≠0,∴![]() 。
。
(3)由(2)知,顶点在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为:
上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为:![]() ,即
,即![]() 。
。
对于顶点在在直线![]() 上的一点Am(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
上的一点Am(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
若点Dm在某一抛物线![]() 上,则
上,则
![]() ,化简,得
,化简,得![]() 。
。
∵m,n为正整数,且m≤n≤12,∴n=4,8,12,m=3,6,9。
∴所有满足条件的正方形边长为3,6,9。
(1)当顶点坐标为(1,1)时,由抛物线顶点坐标公式,有 ,即
,即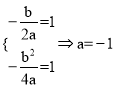 。
。
当顶点坐标为(m,m),m≠0时,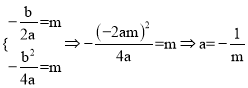 。
。
(2)根据点在直线上,点的坐标满足方程的关系,将抛物线顶点坐标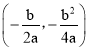 代入
代入![]() ,
,
化简即可用含k的代数式表示b。
由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标。
(3)将依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),将(2 m,m)代入抛物线![]() 求出m,n的关系,即可求解。
求出m,n的关系,即可求解。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=14x2+1(如图所示).
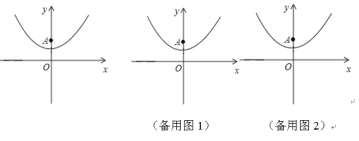
(1)填空:抛物线的顶点坐标是(___,___),对称轴是___;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B. 若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上。在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点(-1,2)和(1,0),且与y
的图象开口向上,图象经过点(-1,2)和(1,0),且与y
轴相交于负半轴。给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序
,其中正确结论的序
号是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
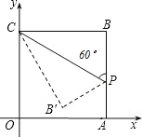
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校国”的目标,兴义市某学校开展了多场足球比赛在某场比赛中,一个足球被从地面向上踢出,它距地面的高度h(m)可以用公式h=﹣5t2+v0t表示,其中t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果要求足球的最大高度达到20m,那么足球被踢出时的速度应该达到( )
A. 5m/s B. 10m/s C. 20m/s D. 40m/s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,
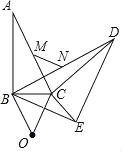
(1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是 (填写序号即可);
(2)判断∠A和∠BEC的数量关系,并证明;
(3)点N是BD的中点,连接MN,若MN=2,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com