
【题目】已知关于![]() 的方程
的方程![]() 有两个正整数根(m是正整数),且
有两个正整数根(m是正整数),且![]() 、
、![]() 满足
满足![]() ,
,![]() 。
。
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
【答案】(1)2 (2)2或6
【解析】
(1)本题可先求出方程![]() 的两个根,然后根据这两个根都是正整数求出m的值.
的两个根,然后根据这两个根都是正整数求出m的值.
(2)由(1)得出的m的值,然后将![]() ,
,![]() .进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
.进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
(1)∵关于x的方程(m2﹣1)x2﹣3(3m﹣1)x+18=0有两个正整数根(m是整数).
∵a=m2﹣1,b=﹣9m+3,c=18,
∴b2﹣4ac=(9m﹣3)2﹣72(m2﹣1)=9(m﹣3)2≥0,
设x1,x2是此方程的两个根,
∴![]()
∴![]() 也是正整数,即m2﹣1=1或2或3或6或9或18,
也是正整数,即m2﹣1=1或2或3或6或9或18,
又∵m为正整数,∴m=2;
(2)把m=2代入两等式,化简得![]() ,
,![]()
当a=b时, ![]() =2,
=2,
当a≠b时,a、b是方程![]() 的两根,而△>0,由韦达定理得a+b=4>0,ab=2>0,则a>0、b>0.
的两根,而△>0,由韦达定理得a+b=4>0,ab=2>0,则a>0、b>0.
![]() =
=![]() .
.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线解析式可以是![]() 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a= ;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是 ;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线![]() 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线![]() 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
查看答案和解析>>
科目:初中数学 来源: 题型:
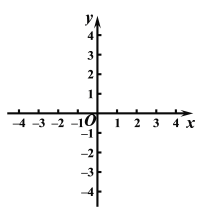
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
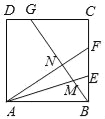
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是 .
S四边形ANGD.其中正确的结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2, ![]() ,求线段DC的长;
,求线段DC的长;
(2)求证:EF·GB=BF·GE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
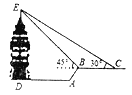
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com