
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
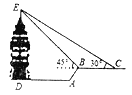
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
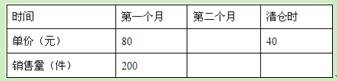
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
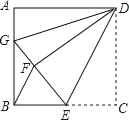
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE,使点B落在点F处,连接AF,则当线段AF的长取最小值时,tan∠FBD是____.
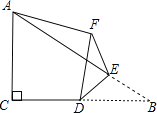
查看答案和解析>>
科目:初中数学 来源: 题型:
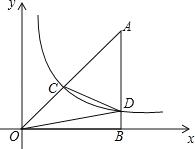
【题目】如图,△OAB中,∠ABO=90°,点A位于第一象限,点O为坐标原点,点B在x轴正半轴上,若双曲线y=![]() (x>0)与△OAB的边AO.AB分别交于点C.D,点C为AO的中点,连接OD.CD.若S△OBD=3,则S△OCD为_____.
(x>0)与△OAB的边AO.AB分别交于点C.D,点C为AO的中点,连接OD.CD.若S△OBD=3,则S△OCD为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
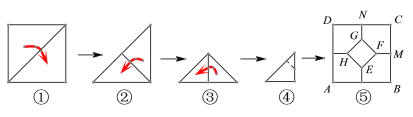
【题目】将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM、GN是折痕,若正方形EFGH与五边形MCNGF面积相等,则![]() 的值是____________
的值是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
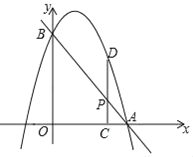
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M和点N的坐标;
②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;
③是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com