
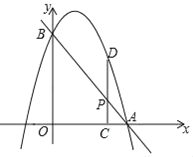
【题目】如图,已知直线y=﹣2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣2x2+2x+4,设其顶点为M,其对称轴交AB于点N.
①求点M和点N的坐标;
②在抛物线的对称轴上找一点Q,使|AQ﹣BQ|的值最大,请直接写出点Q的坐标;
③是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1)①N(![]() ,3);②Q(
,3);②Q(![]() ,6);③不存在,理由见解析;(4)y=﹣2x2+2x+4或y=﹣
,6);③不存在,理由见解析;(4)y=﹣2x2+2x+4或y=﹣![]() x2+3x+4.
x2+3x+4.
【解析】
(1)①函数的对称轴为:x=-![]() =
=![]() ,故点M(
,故点M(![]() ,
,![]() ),即可求解;
),即可求解;
②设抛物线与x轴左侧的交点为R(-1,0),则点A与R关于抛物线的对称轴对称,连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,即可求解;
③四边形MNPD为菱形,首先PD=MN,即(-2x2+2x+4)-(-2x+4)=![]() ,解得:x=
,解得:x=![]() 或
或![]() (舍去
(舍去![]() ),故点P(
),故点P(![]() ,1),而PN=
,1),而PN=![]() =
=![]() ≠MN,即可求解;
≠MN,即可求解;
(2)分∠DBP为直角、∠BDP为直角两种情况,分别求解即可.
(1)①函数的对称轴为:x=﹣![]() =
=![]() ,故点M(
,故点M(![]() ,
,![]() ),
),
当x=![]() 时,y=﹣2x+4=3,故点N(
时,y=﹣2x+4=3,故点N(![]() ,3);
,3);
②设抛物线与x轴左侧的交点为R(﹣1,0),则点A与R关于抛物线的对称轴对称,
连接RB并延长交抛物线的对称轴于点Q,则点Q为所求,
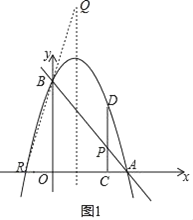
将R、B的坐标代入一次函数表达式:y=kx+b并解得:
直线RB的表达式为:y=4x+4,
当x=![]() 时,y=6,
时,y=6,
故点Q(![]() ,6);
,6);
③不存在,理由:
设点P(x,﹣2x+4),则点D(x,﹣2x2+2x+4),
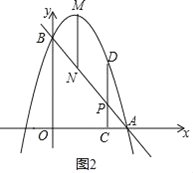
MN=![]() ﹣3=
﹣3=![]() ,
,
四边形MNPD为菱形,首先PD=MN,
即(﹣2x2+2x+4)﹣(﹣2x+4)=![]() ,解得:x=
,解得:x=![]() 或
或![]() (舍去
(舍去![]() ),
),
故点P(![]() ,1),而PN=
,1),而PN=![]() =
=![]() ≠MN,
≠MN,
故不存在点P,使四边形MNPD为菱形;
(2)当点P的横坐标为1时,则其坐标为:(1,2),此时点A、B的坐标分别为:(2,0)、(0,4),
①当∠DBP为直角时,以B、P、D为顶点的三角形与△AOB相似,
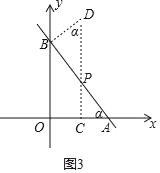
则∠BAO=∠BDP=α,tan∠BAO=![]() =2=tanα,则sinα=
=2=tanα,则sinα=![]() ,
,
PA=![]() ,PB=AB﹣PA=2
,PB=AB﹣PA=2![]() ﹣
﹣![]() =
=![]() ,
,
则PD=![]() =
=![]() ,故点D(1,
,故点D(1,![]() );
);
②当∠BDP为直角时,以B、P、D为顶点的三角形与△AOB相似,
则BD∥x轴,则点B、D关于抛物线的对称轴对称,故点D(1,4),
综上,点D的坐标为:(1,4)或(1,![]() ),
),
将点A、B、D的坐标代入抛物线表达式:y=ax2+bx+c,
解得:y=﹣2x2+2x+4或y=﹣![]() x2+3x+4.
x2+3x+4.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
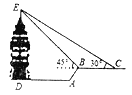
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
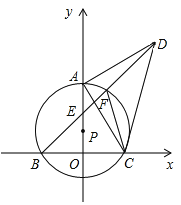
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4![]() ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF, ![]() 经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
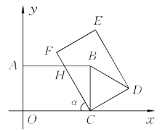
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一个动点,过点
边上一个动点,过点![]() 作
作![]() 交边
交边![]() 于
于![]() ,过点
,过点![]() 作射线
作射线![]() 交
交![]() 边于点
边于点![]() ,交射线
,交射线![]() 于点
于点![]() ,联结
,联结![]() .设
.设![]() 两点的距离为
两点的距离为![]() ,
,![]() 两点的距离为
两点的距离为![]() .
.
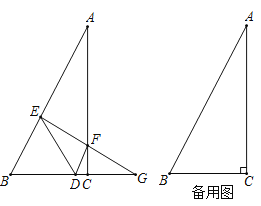
(1)求证:![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)点![]() 在运动过程中,
在运动过程中,![]() 能否构成等腰三角形?如果能,请直接写出
能否构成等腰三角形?如果能,请直接写出![]() 的长,如果不能,请简要说明理由.
的长,如果不能,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com