
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
【答案】(1)函数图象与x轴的交点坐标为(2﹣![]() ,0),(2+
,0),(2+![]() ,0);(2)此时函数的最小值为﹣2;(3)k≥3.
,0);(2)此时函数的最小值为﹣2;(3)k≥3.
【解析】
(1)令y=0,得到关于x的方程,解方程即可;
(2)分两种情况讨论求得即可;
(3)由题意可知![]() ,解不等式即可求得.
,解不等式即可求得.
解:(1)∵k=3,
∴y=x2﹣4x+2,
令y=0,则x2﹣4x+2=0,
解得x=2±![]() ,
,
∴函数图象与x轴的交点坐标为(2﹣![]() ,0),(2+
,0),(2+![]() ,0);
,0);
(2)∵函数图象的对称轴与原点的距离为2,
∴![]() =±2,
=±2,
解得k=3或﹣1,
当对称轴为直线x=﹣2时,则k=﹣1,
把x=﹣1代入得,y=﹣1,
∴此时函数的最小值为﹣1;
当对称轴为x=2时,则k=3,
∵y=x2﹣4x+2=(x﹣2)2﹣2
∴此时函数的最小值为﹣2;
(3)由二次函数y=x2﹣2(k﹣1)x+2可知B(0,2),开口向上,
设二次函数图象上的一点P(x,y),若满足0≤x≤4时,y≤2,则![]() ≥2
≥2
∴k≥3.


科目:初中数学 来源: 题型:
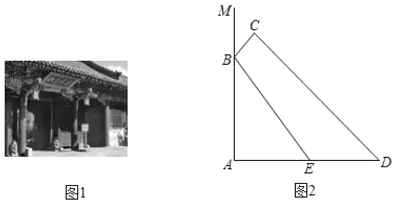
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
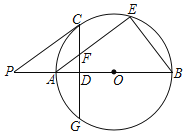
【题目】如图,AB为⊙O的直径,AE是⊙O的弦,C是弧AE的中点,弦CG⊥AB于点D,交AE于点F,过点C作⊙O的切线,交BA延长线于点P,连接BE
(1)求证:PC∥AE;
(2)若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生身体素质,某校决定开展足球、篮球、排球、兵乓球等四项课外体育活动,要求全员参与,并且每名学生只能选择其中一项.为了解选择各种体育活动项目的学生人数,该校随机抽取了部分学生进行调查,并绘制出如下两幅不完整的统计图,请根据统计图回答下列问题:
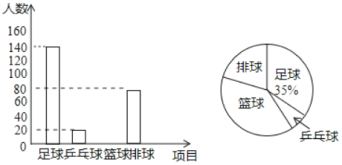
(1)直接写出这次抽样调查的学生人数;
(2)补全条形统计图;
(3)若该学校总人数是1500人,请估计选择篮球项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,E,F分别是边AB,CD的中点,M,N分别是边AD,AB上两点,将△AMN沿MN对折,使点A落在点E上.若AB=a,BC=b,且N是FB的中点,则![]() 的值为____.
的值为____.
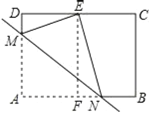
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
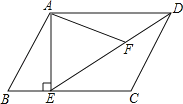
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3![]() ,AE=3,求AF的长;
,AE=3,求AF的长;
(3)若CD=CE,则直线CD是以点E为圆心,AE长为半径的圆的切线.试证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
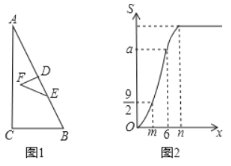
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设
,设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
关于![]() 的函数图象如图2所示(其中
的函数图象如图2所示(其中![]() ,
,![]() ,
,![]() ,
,![]() 时,函数的解析式不同).则
时,函数的解析式不同).则![]() __.
__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com