
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设
,设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
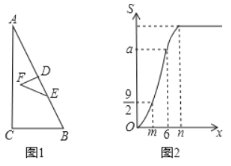
关于![]() 的函数图象如图2所示(其中
的函数图象如图2所示(其中![]() ,
,![]() ,
,![]() ,
,![]() 时,函数的解析式不同).则
时,函数的解析式不同).则![]() __.
__.
【答案】![]()
【解析】
当点F在AC上时,先求此时DF=3,由已知的图2知:当x=m=3时,S=![]() ,即当0<x≤3时,点F在AC上时,S最大,在这一取值重叠部分是△EDF,图2中最后一个阶段:计算当EF过点C时,所对应的DE的长,就是n的值,作辅助线,构建等腰直角三角形CHE,先根据面积法求高线CH的长,再分别求DH和EH的长,可得x的值,即n的值.
,即当0<x≤3时,点F在AC上时,S最大,在这一取值重叠部分是△EDF,图2中最后一个阶段:计算当EF过点C时,所对应的DE的长,就是n的值,作辅助线,构建等腰直角三角形CHE,先根据面积法求高线CH的长,再分别求DH和EH的长,可得x的值,即n的值.
解:(1)∵DE=x,
由旋转可得:△DEF是等腰三角形,
∴![]()
由已知图2得:![]() ,
,
解得:![]()
∵m>0,
∴m=3,
当点F在AC上时,如图1,DE=DF=3,
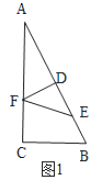
∵BD=6,即当x=6时,点E与B重合,如图2,

此时,DG=3,GF=6-3=3,
∵D是AB的中点,
∴AD=BD=6,
tan∠DGA=tan∠MGH=![]()
∴MH=2MG,
∵∠F=45°,
∴△MHF是等腰直角三角形,
∴FM=MH=2MG,
∵FG=3,
∴FM=MH=2,
∴![]()
∴a=15,
当EF经过点C时,如图3,过C作CH⊥AB于H,

![]()
∵AB=12,
∴![]()
∴![]() ,即
,即![]() ,
,![]()
∵∠AEC=45°,
∴△CHE是等腰直角三角形,
∴![]()
∴![]()
∴![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间(用t表示,单位:小时),采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如下图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如下图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
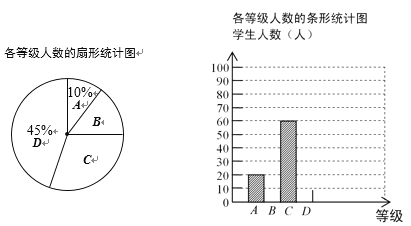
(1)求本次调查的学生人数;
(2)求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
(3)若该校共有学生1200人,试估计每周课外阅读时间不少于3小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮![]() 个,该文具厂每天生产成本为
个,该文具厂每天生产成本为![]() 元.
元.
(1)求橡皮和水笔的销售单价;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年全民抗疫期间,抗疫志士莫小贝购进一条生产线生产抗疫物质. 已知该生产线的三个操作平台分别排列在同一直线上,顺次是甲、乙、丙,其中甲乙平台之间的距离为40米,乙丙平台之间的距离为60米,操作甲、乙、丙平台分别需要20人、70人、60人. 由于时间仓促无法做到完全自动化,需要在三个平台之间建立一个原材料供给站让工人自取,有如下两个方案:方案一:让所有工人到供给站的距离总和最小;方案二:让甲、丙平台所有工人到供给站的距离之和等于乙平台所有工人到供给站的距离之和.
(1)若按照方案一建站,供给站距离甲平台多少米?
(2)若按照方案二建站,供给站距离甲平台多少米?
(3)在(2)的条件下,若甲平台的工人数增加![]() 人(
人(![]() ),那么随着
),那么随着![]() 的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AE∥BD交射线CB于点E.
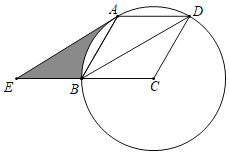
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中线段AE、线段BE和![]() 围成的部分的面积.
围成的部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com