
【题目】如图,在![]() 中,
中,![]() 与
与![]() 相切于点
相切于点![]() ,直径
,直径![]() 与
与![]() 交于点
交于点![]() ,弦
,弦![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为________.
的长为________.
【答案】![]()
【解析】
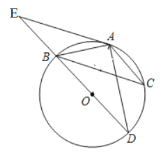
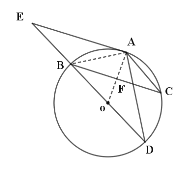
连接OA,AB,根据∠CAD和∠E的度数,以及同弧所对的圆周角相等得出∠CBD=∠E,从而得到AE∥BC,可得△OAB为等边三角形,利用垂径定理得出AB=AC,BF=CF,结合BC=2与勾股定理求出AB和BO的长, 即可得到结果.
解:连接OA,AB,F为AO和BC的交点,
∵∠CAD=∠E=30°,
∴∠CBD=∠E=30°,
∴AE∥BC,
∵AE与圆O相切,
∴AO⊥AE,
∴∠OAE=∠BFO=90°,
∴∠BOF=60°,
∴△OAB为等边三角形,
∵OA⊥BC,BC=2,
∴OA垂直平分BC,
∴BF=CF=1,设OF=x,则OB=2x,
在△BOF中,有![]() ,
,
解得:x=![]() ,
,
∴AB=AC=2x=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设
,设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
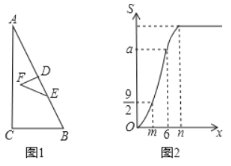
关于![]() 的函数图象如图2所示(其中
的函数图象如图2所示(其中![]() ,
,![]() ,
,![]() ,
,![]() 时,函数的解析式不同).则
时,函数的解析式不同).则![]() __.
__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′ E处,AD′ 与CE交于点F,若∠B=55°,∠DAE=20°,则∠FED′ 的大小为( )
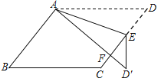
A.20°B.30°
C.35°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN,设运动时间为t(s)﹙0<t<4﹚,解答下列问题:
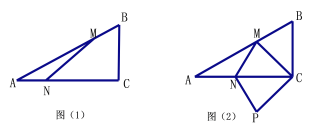
⑴设△AMN的面积为S,求S与t之间的函数关系式,并求出S的最大值;
⑵如图⑵,连接MC,将△MNC沿NC翻折,得到四边形MNPC,当四边形MNPC为菱形时,求t的值;
⑶当t的值为 ,△AMN是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的内角,
的内角,![]() ,
,

(1)![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,判断四边形
,判断四边形![]() 的形状:________;
的形状:________;
(2)旋转![]() 到
到![]() ,如图2,边
,如图2,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,AE=AF.过点
,AE=AF.过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .问:
.问:![]() 是否平分
是否平分![]() .若是请证明,若不是请说明理由.
.若是请证明,若不是请说明理由.
(3)四边形![]() 在(2)的条件下,若恰好
在(2)的条件下,若恰好![]() ,如图3.连接
,如图3.连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一个动点.
上的一个动点.
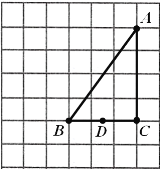
(1)当点![]() 为线段
为线段![]() 中点时,
中点时,![]() 的长度等于__________;
的长度等于__________;
(2)将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() ,连
,连![]() ,当线段
,当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点
取得最小值时,请借助无刻度直尺在给定的网格中画出点![]() ,点
,点![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ,点
,点![]() 的:____________________.
的:____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
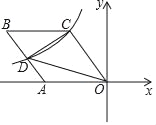
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=﹣
,反比例函数y=﹣![]() 的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
的图象经过点C,与AB交与点D,则△COD的面积的值等于_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图![]() 正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
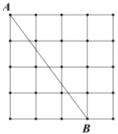
(1)在图中画出一个直角![]() ,并且其面积为5;
,并且其面积为5;
(2)在图中画出一个等腰直角![]() ;
;
(3)连接![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com