
【题目】如图1,![]() 是
是![]() 的内角,
的内角,![]() ,
,

(1)![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,判断四边形
,判断四边形![]() 的形状:________;
的形状:________;
(2)旋转![]() 到
到![]() ,如图2,边
,如图2,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,AE=AF.过点
,AE=AF.过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .问:
.问:![]() 是否平分
是否平分![]() .若是请证明,若不是请说明理由.
.若是请证明,若不是请说明理由.
(3)四边形![]() 在(2)的条件下,若恰好
在(2)的条件下,若恰好![]() ,如图3.连接
,如图3.连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
【答案】(1)菱形;(2)![]() 平分
平分![]() ;理由见解析;(3)证明见解析
;理由见解析;(3)证明见解析
【解析】
(1)根据平行四边形的定义可得四边形ABFG为平行四边形,然后证出△FAB为等边三角形可得BF=BA,从而得出结论;
(2)过点![]() 作
作![]() 于N,作
于N,作![]() 于M,先证出
于M,先证出![]() 是等边三角形,然后利用SAS证出
是等边三角形,然后利用SAS证出![]() ,从而得出
,从而得出![]() ,然后根据角平分线的判定即可证出结论;
,然后根据角平分线的判定即可证出结论;
(3)先证出平行四边形![]() 是菱形,从而得出
是菱形,从而得出![]() ,然后设
,然后设![]() 、
、![]() 交于点
交于点![]() ,根据30°所对的直角边是斜边的一半即可得出
,根据30°所对的直角边是斜边的一半即可得出![]() ,然后结合平行四边形的性质和等角对等边即可证出结论.
,然后结合平行四边形的性质和等角对等边即可证出结论.
解:(1)∵![]() ,
,![]()
∴四边形ABFG为平行四边形
∵![]() 中,
中,![]()
∴∠ABC=180°-∠DAB=120°
∵![]() 平分
平分![]() ,
,
∴∠ABF=![]() =60°
=60°
∴∠AFB=180°-∠ABF-∠FAB=60°
∴△FAB为等边三角形
∴BF=BA
∴四边形ABFG为菱形
故答案为:菱形;
(2)答:![]() 平分
平分![]()
理由:过点![]() 作
作![]() 于N,作
于N,作![]() 于M
于M
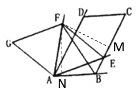
∴![]()
∵由题意得:![]() , AE=AF
, AE=AF
∴![]() 是等边三角形
是等边三角形
∴![]()
∴![]()
∵![]()
即:![]()
∵在![]() 中,
中,![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
又∵![]() ,作
,作![]()
∴![]() 平分
平分![]()
(3)∵![]() ,
,![]()
∴四边形![]() 是平行四边形
是平行四边形
∵由(2)知![]()
∴平行四边形![]() 是菱形
是菱形
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() ,
,
∴![]() ,
,![]()
设![]() 、
、![]() 交于点
交于点![]()
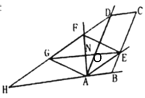
在![]() 中,
中,![]()
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵![]() ,
,
∵四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴四边形![]() 为平行四边形,
为平行四边形,
又∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
∵![]()
∴![]()
∴![]()
∴![]()


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮![]() 个,该文具厂每天生产成本为
个,该文具厂每天生产成本为![]() 元.
元.
(1)求橡皮和水笔的销售单价;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AE=![]() ,求AC长.
,求AC长.
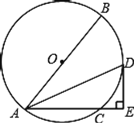
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
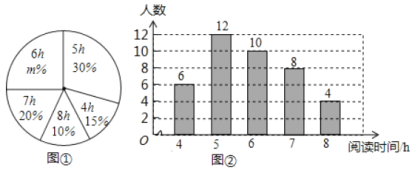
(Ⅰ)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个根.其中正确的有( )
的一个根.其中正确的有( )
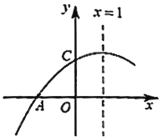
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
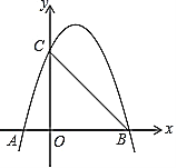
(1)求抛物线的解析式;
(2)设点![]() 在第一象限的抛物线上,连接
在第一象限的抛物线上,连接![]() ,
,![]() .试问,在对称轴左侧的抛物线是否存在一点
.试问,在对称轴左侧的抛物线是否存在一点![]() ,满足
,满足![]() ?如果存在,请求出点
?如果存在,请求出点![]() 的坐标:如果不存在,请明理由;
的坐标:如果不存在,请明理由;
(3)存在正实数![]() ,
,![]() (
(![]() ),当
),当![]() 时,恰好满足
时,恰好满足![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了![]() .
.
(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?
(2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为![]() 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线交![]() 轴正半轴于点
轴正半轴于点![]() (1,0)和点
(1,0)和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
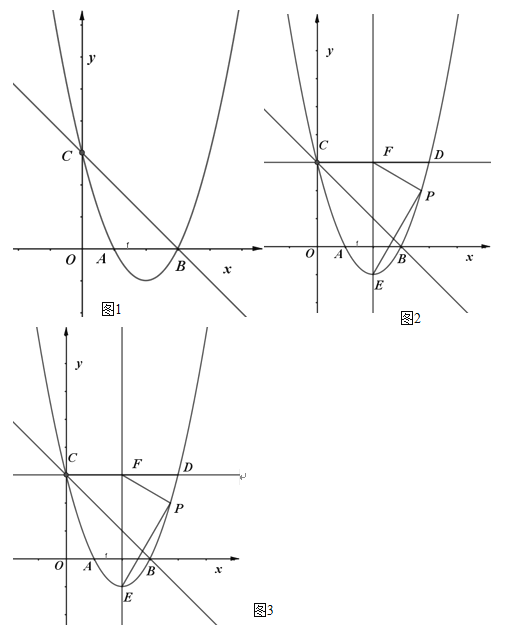
(1)如图1,直线![]() 经过点
经过点![]() 、点
、点![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)如图2,点![]() 为该抛物线
为该抛物线![]() 的顶点,过点
的顶点,过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() ,该抛物线对称轴右侧的抛物线上有一点
,该抛物线对称轴右侧的抛物线上有一点![]() ,当
,当![]() 时,求
时,求![]() 点的纵坐标.
点的纵坐标.
(3)如图3,在(1)(2)的结论下,抛物线对称轴右侧的抛物线上有一点![]() ,作
,作![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com