
【题目】如图,在平面直角坐标系中,抛物线交![]() 轴正半轴于点
轴正半轴于点![]() (1,0)和点
(1,0)和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
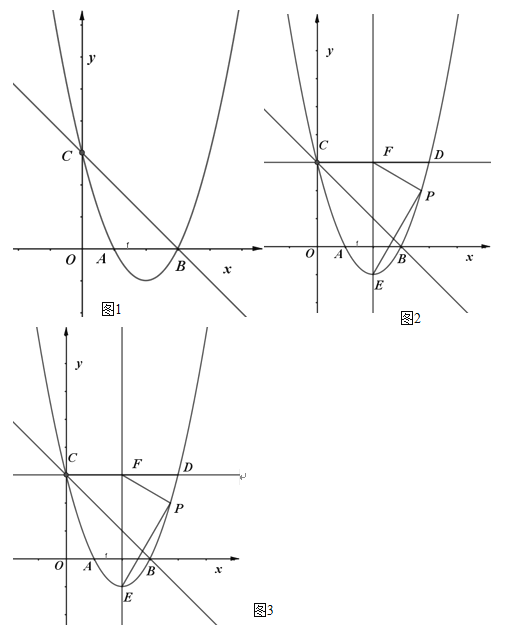
(1)如图1,直线![]() 经过点
经过点![]() 、点
、点![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)如图2,点![]() 为该抛物线
为该抛物线![]() 的顶点,过点
的顶点,过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() ,该抛物线对称轴右侧的抛物线上有一点
,该抛物线对称轴右侧的抛物线上有一点![]() ,当
,当![]() 时,求
时,求![]() 点的纵坐标.
点的纵坐标.
(3)如图3,在(1)(2)的结论下,抛物线对称轴右侧的抛物线上有一点![]() ,作
,作![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;(2)点P的纵坐标为2;(3)
;(2)点P的纵坐标为2;(3)![]() 点的坐标为(
点的坐标为(![]() ,11).
,11).
【解析】
(1)由直线的解析式,先求出点B、C的坐标,结合点A的坐标,利用待定系数法即可得到答案;
(2)把点A代入,求出n的值,然后得到点C和点E的坐标,然后求出点F的坐标,设点P为(x,![]() ),由
),由![]() ,即可求出点P的横坐标,即可求出点P的纵坐标;
,即可求出点P的横坐标,即可求出点P的纵坐标;
(3)过点P作PI⊥GH于点I,先求出直线PE的解析式,得到PK=2PI,然后设点G为(m,![]() ),表示出GK的长度,结合
),表示出GK的长度,结合![]() ,得到关于m的一元二次方程,解方程求出m的值,即可得到答案.
,得到关于m的一元二次方程,解方程求出m的值,即可得到答案.
解:(1)∵![]() 经过点
经过点![]() 、点
、点![]() ,
,
∴令![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
∴点B为(3,0),点C为(0,3),
设抛物线的解析式为![]() ,
,
把点A、B、C,三点代入解析式,得:
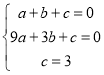 ,解得:
,解得: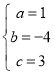 ,
,
∴![]() ;
;
(2)∵点A(1,0)在抛物线![]() 图像上,则
图像上,则
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴顶点E为(2,![]() ),
),
令x=0,则![]() ,
,
∴点C为(0,3),
∵EF垂直平分CD,
∴点D的坐标为(4,3),点F的坐标为(2,3),
∵点P在抛物线![]() 上,则设点P为(x,
上,则设点P为(x,![]() ),
),
又∵E为(2,![]() ),F为(2,3),
),F为(2,3),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵点P在对称轴右侧,则![]() ,
,
∴点P的横坐标为![]() ,
,
∴点P的纵坐标为:
![]() ;
;
(3)如图:过点P作PI⊥GH于点I,
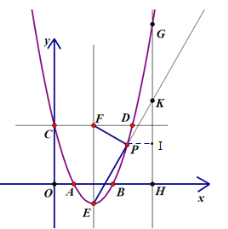
∵点E(2,![]() ),点P为(
),点P为(![]() ,2),
,2),
∴可求出直线PE的解析式为:![]() ,
,
∴∠KPI=60°,
∵PI⊥GH,
∴∠KIP=90°,∠PKI=30°,
∴PK=2PI,
∵点G在抛物线![]() 图像上,
图像上,
则设点G为(m,![]() ),
),
∴点K的坐标为(m,![]() )
)
∴GK=![]() ;
;
∵第P的坐标为(![]() ,2),
,2),
∴点I的坐标为(m,![]() ),
),
∴PI=![]() ,
,
∴PK=![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
当![]() 时,点G与点P、点K重合,
时,点G与点P、点K重合,
∴![]() ;不符合题意,舍去;
;不符合题意,舍去;
∴点G的横坐标为![]() ;
;
∴点G的纵坐标为:![]() ,
,
∴点G的坐标为(![]() ,11).
,11).


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的内角,
的内角,![]() ,
,

(1)![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,判断四边形
,判断四边形![]() 的形状:________;
的形状:________;
(2)旋转![]() 到
到![]() ,如图2,边
,如图2,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,AE=AF.过点
,AE=AF.过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .问:
.问:![]() 是否平分
是否平分![]() .若是请证明,若不是请说明理由.
.若是请证明,若不是请说明理由.
(3)四边形![]() 在(2)的条件下,若恰好
在(2)的条件下,若恰好![]() ,如图3.连接
,如图3.连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为:![]() (物理)、
(物理)、![]() (化学)、
(化学)、![]() (生物),每科试题各为
(生物),每科试题各为![]() 道,考生随机抽取其中
道,考生随机抽取其中![]() 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为 ;
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图![]() 正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
正方形网格,每个小正方形的边长为1,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
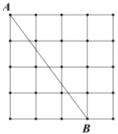
(1)在图中画出一个直角![]() ,并且其面积为5;
,并且其面积为5;
(2)在图中画出一个等腰直角![]() ;
;
(3)连接![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调査的结果绘制成如下的两幅不完整的统计图.
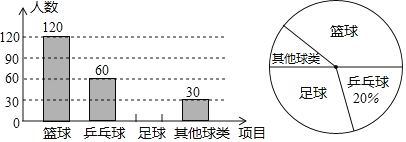
请根据图中提供的信息,解答下面的问题
(1)参加调査的学生共有 人,在扇形图中,表示“其他球类”的扇形圆心角为 度;
(2)将条形图补充完整;
(3)若该校有2300名学生,则估计喜欢“足球”的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
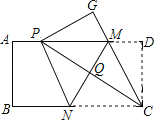
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形AOBC的边AO、OB分别在y轴、x轴正半轴上,点C的坐标为(8,6),点E是x轴上任意一点,连接EC,交AB所在直线于点F,当△ACF为等腰三角形时,EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:(1)如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2),请你写出![]() 、
、![]() 、ab之间的等量关系是______________;
、ab之间的等量关系是______________;
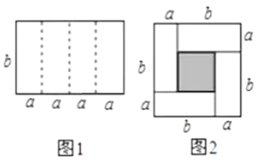
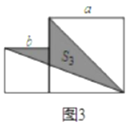
(2)两个边长分别为a和b的正方形如图放置(图3),求出图3中阴影部分的面积![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com