
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一个动点.
上的一个动点.
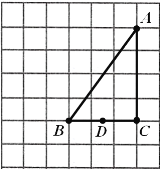
(1)当点![]() 为线段
为线段![]() 中点时,
中点时,![]() 的长度等于__________;
的长度等于__________;
(2)将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() ,连
,连![]() ,当线段
,当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点
取得最小值时,请借助无刻度直尺在给定的网格中画出点![]() ,点
,点![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ,点
,点![]() 的:____________________.
的:____________________.
【答案】(1)![]() ;(2)图见解析;取格点
;(2)图见解析;取格点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,它们分别与网格线相交于点
,它们分别与网格线相交于点![]() ,
,![]() ,取格点
,取格点![]() ,连接
,连接![]()
![]() ,
,![]() ,它们相交于点
,它们相交于点![]() ,则点
,则点![]() 即为所求;取格点
即为所求;取格点![]() ,
,![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解析】
(1)根据勾股定理先求出AB的长,再利用中位线定理可得出DP的长;
(2)如图1,设P为AC上任意一点,过点P′作P′C′⊥CB交其延长线与点C′,易得△CDP≌△C′P′D,得出P′C′=CD=![]() ,从而可得出点P′一定在直线l上,再找出点B关于直线l的对称点K,连接DK与l的交点即可点P′,此时
,从而可得出点P′一定在直线l上,再找出点B关于直线l的对称点K,连接DK与l的交点即可点P′,此时![]() 的值最小,因此根据平行四边形的判定与性质以及全等三角形的判定与性质先作出直线l(或在直线l上的线段),利用轴对称的性质可得出点K,进而可得出点
的值最小,因此根据平行四边形的判定与性质以及全等三角形的判定与性质先作出直线l(或在直线l上的线段),利用轴对称的性质可得出点K,进而可得出点![]() ;利用旋转的性质以及全等三角形的判定与性质在AC上找一点P,使△CDP≌△QKP′,则有DP=KP′=DP′,即可得出点P.
;利用旋转的性质以及全等三角形的判定与性质在AC上找一点P,使△CDP≌△QKP′,则有DP=KP′=DP′,即可得出点P.
解:(1)根据勾股定理得,AB=![]() ,
,
又点D为BC的中点,点P为AC的中点,
∴DP为△ABC的中位线,
∴DP=![]() AB=
AB=![]() .
.
故答案为:![]() ;
;
(2)如图1,设P为AC上任意一点,过点P′作P′C′⊥CB交其延长线与点C′,
根据题意可得,DP=DP′,∠PDP′=90°,
∴易得△CDP≌△C′P′D,∴P′C′=CD=![]() ,
,
∴点P′一定在直线l上,
∴再找出点B关于直线l的对称点K,连接DK与l的交点即可点P′,此时![]() 的值最小.
的值最小.

如图2,取格点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,它们分别与网格线相交于点
,它们分别与网格线相交于点![]() ,
,![]() ,取格点
,取格点![]() ,连接
,连接![]() ,
,![]() ,它们相交于点
,它们相交于点![]() ,则点
,则点![]() 即为所求;
即为所求;
取格点![]() ,
,![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
故答案为:取格点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,它们分别与网格线相交于点
,它们分别与网格线相交于点![]() ,
,![]() ,取格点
,取格点![]() ,连接
,连接![]() ,
,![]() ,它们相交于点
,它们相交于点![]() ,则点
,则点![]() 即为所求;取格点
即为所求;取格点![]() ,
,![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,连接
,连接![]() ,与网格线相交于点
,与网格线相交于点![]() ,则点
,则点![]() 即为所求.
即为所求.


科目:初中数学 来源: 题型:
【题目】2020年全民抗疫期间,抗疫志士莫小贝购进一条生产线生产抗疫物质. 已知该生产线的三个操作平台分别排列在同一直线上,顺次是甲、乙、丙,其中甲乙平台之间的距离为40米,乙丙平台之间的距离为60米,操作甲、乙、丙平台分别需要20人、70人、60人. 由于时间仓促无法做到完全自动化,需要在三个平台之间建立一个原材料供给站让工人自取,有如下两个方案:方案一:让所有工人到供给站的距离总和最小;方案二:让甲、丙平台所有工人到供给站的距离之和等于乙平台所有工人到供给站的距离之和.
(1)若按照方案一建站,供给站距离甲平台多少米?
(2)若按照方案二建站,供给站距离甲平台多少米?
(3)在(2)的条件下,若甲平台的工人数增加![]() 人(
人(![]() ),那么随着
),那么随着![]() 的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )交直线
)交直线![]() :
:![]() 于点
于点![]() ,点
,点![]() 两点,且过点
两点,且过点![]() ,连接
,连接![]() ,
,![]() .
.
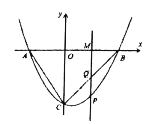
(1)求此抛物线的表达式与顶点坐标;
(2)点![]() 是第四象限内抛物线上的一个动点,过点
是第四象限内抛物线上的一个动点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,试探究点
,试探究点![]() 在运动过程中,是否存在这样的点
在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)若点![]() 在
在![]() 轴上,点
轴上,点![]() 在抛物线上,是否存在以点
在抛物线上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的平行四边形?若存在,求点
为顶点的平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
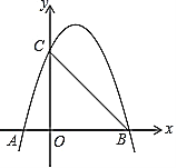
(1)求抛物线的解析式;
(2)设点![]() 在第一象限的抛物线上,连接
在第一象限的抛物线上,连接![]() ,
,![]() .试问,在对称轴左侧的抛物线是否存在一点
.试问,在对称轴左侧的抛物线是否存在一点![]() ,满足
,满足![]() ?如果存在,请求出点
?如果存在,请求出点![]() 的坐标:如果不存在,请明理由;
的坐标:如果不存在,请明理由;
(3)存在正实数![]() ,
,![]() (
(![]() ),当
),当![]() 时,恰好满足
时,恰好满足![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店第一次用1200元购进一批大樱桃,很快售完;又用2500元购进第二批大樱桃,所购公斤数是第一批的2倍,但进价比第一批每公斤多了5元.
(1)求第一批大樱桃每公斤进价多少元?
(2)若以每公斤150元的价格销售第二批大樱桃,售出![]() 后,为了尽快售完,决定打折促销,要使第二批大樱桃的销售利润不少于320元,剩余的大樱桃每公斤售价至少打几折(利润=售价-进价)?
后,为了尽快售完,决定打折促销,要使第二批大樱桃的销售利润不少于320元,剩余的大樱桃每公斤售价至少打几折(利润=售价-进价)?
查看答案和解析>>
科目:初中数学 来源: 题型:
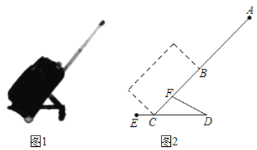
【题目】如图①,图②分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆![]() 、箱长
、箱长![]() 、拉杆
、拉杆![]() 的长度都相等,即
的长度都相等,即![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,点
上,点![]() 在
在![]() 上,支杆
上,支杆![]() ,
,![]() ,
,![]() ,
,![]() .
.
请根据以上信息,解决下列问题;
(1)求![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)求拉杆端点![]() 到水平滑杆
到水平滑杆![]() 的距离(结果保留到
的距离(结果保留到![]() ).
).
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com