
【题目】2020年全民抗疫期间,抗疫志士莫小贝购进一条生产线生产抗疫物质. 已知该生产线的三个操作平台分别排列在同一直线上,顺次是甲、乙、丙,其中甲乙平台之间的距离为40米,乙丙平台之间的距离为60米,操作甲、乙、丙平台分别需要20人、70人、60人. 由于时间仓促无法做到完全自动化,需要在三个平台之间建立一个原材料供给站让工人自取,有如下两个方案:方案一:让所有工人到供给站的距离总和最小;方案二:让甲、丙平台所有工人到供给站的距离之和等于乙平台所有工人到供给站的距离之和.
(1)若按照方案一建站,供给站距离甲平台多少米?
(2)若按照方案二建站,供给站距离甲平台多少米?
(3)在(2)的条件下,若甲平台的工人数增加![]() 人(
人(![]() ),那么随着
),那么随着![]() 的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
【答案】(1) 按方案一建站,供给站应建在距离甲平台40米处;(2)按方案二建站,供给站应建在距离甲平台80米处;(3)供给站将离甲平台越来越远,理由见解析.
【解析】
(1)设供给站距离甲平台![]() 米,所有工人的距离之和为
米,所有工人的距离之和为![]() 米,分情况讨论:当供给站建在甲乙平台之间即
米,分情况讨论:当供给站建在甲乙平台之间即![]() 时,当供给站建在乙丙平台之间即
时,当供给站建在乙丙平台之间即![]() 时,分别列出y关于x的函数关系式,求得相应的最小值比较即可得到答案;
时,分别列出y关于x的函数关系式,求得相应的最小值比较即可得到答案;
(2)分情况讨论,根据题意列出相应的方程求解后比较即可得到答案;
(3)分情况讨论,根据题意列出相应的方程求解后,再判断x的值随a 的值的变化情况由此即可得到答案.
(1)设供给站距离甲平台![]() 米,所有工人的距离之和为
米,所有工人的距离之和为![]() 米
米
①当供给站建在甲乙平台之间即![]() 时
时
![]()
∴当![]() 时,
时,![]() 取得最小值4400
取得最小值4400
②当供给站建在乙丙平台之间即![]() 时
时
![]()
∵![]() 随
随![]() 增大而增大,并且当
增大而增大,并且当![]() 时,
时,![]()
∴本阶段![]() 的值均大于4400.
的值均大于4400.
综上所述:按方案一建站,供给站应建在距离甲平台40米处
(2)①当![]() 时
时![]()
解得![]() (不在三个平台之间,不合题意,舍去).
(不在三个平台之间,不合题意,舍去).
②当![]() 时
时![]()
解得![]()
综上所述:按方案二建站,供给站应建在距离甲平台80米处
(3)供给站将离甲平台越来越远,理由如下:
①当![]() 时
时![]()
解得![]() (不在三个平台之间,不合题意,舍去).
(不在三个平台之间,不合题意,舍去).
②当![]() 时
时![]()
解得![]()
∴![]() 随着
随着![]() 的增大而增大
的增大而增大
即随着![]() 的增大供给站将离甲平台越来越远.
的增大供给站将离甲平台越来越远.


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
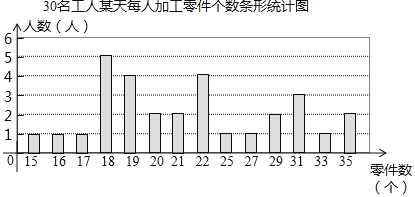
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
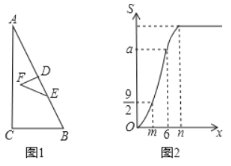
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 为
为![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一点,将
上一点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设
,设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
关于![]() 的函数图象如图2所示(其中
的函数图象如图2所示(其中![]() ,
,![]() ,
,![]() ,
,![]() 时,函数的解析式不同).则
时,函数的解析式不同).则![]() __.
__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与抛物线
的图象与抛物线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线交
点,抛物线交![]() 轴的另一个交点为点
轴的另一个交点为点![]() (点
(点![]() 的左边).点
的左边).点![]() 为抛物线上一个动点(且点
为抛物线上一个动点(且点![]() 的横坐标
的横坐标![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
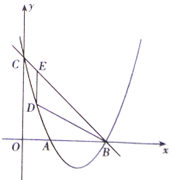
(1)求该抛物线的解析式;
(2)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)在(2)的结论下,点![]() 为抛物线上任意一个动点,点
为抛物线上任意一个动点,点![]() 为
为![]() 轴上一个动点,则以
轴上一个动点,则以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形能否为平行四边形,若能,请直接写出点
四点为顶点的四边形能否为平行四边形,若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
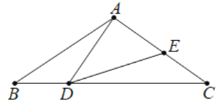
【题目】已知:如图,△ABC中,AB=AC,D,E分别是边BC,AC上的点.且BD=EC,∠ADE=∠B.
(1)求证:AD=DE.
(2)若∠ADE=40°,求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,有以下四个结论:①ab<0,②b<![]() ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
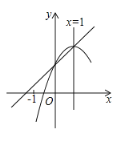
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′ E处,AD′ 与CE交于点F,若∠B=55°,∠DAE=20°,则∠FED′ 的大小为( )
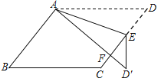
A.20°B.30°
C.35°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一个动点.
上的一个动点.
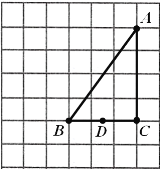
(1)当点![]() 为线段
为线段![]() 中点时,
中点时,![]() 的长度等于__________;
的长度等于__________;
(2)将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() ,连
,连![]() ,当线段
,当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点
取得最小值时,请借助无刻度直尺在给定的网格中画出点![]() ,点
,点![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ,点
,点![]() 的:____________________.
的:____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com