
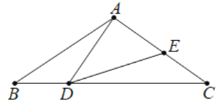
【题目】已知:如图,△ABC中,AB=AC,D,E分别是边BC,AC上的点.且BD=EC,∠ADE=∠B.
(1)求证:AD=DE.
(2)若∠ADE=40°,求∠ADB的度数.
科目:初中数学 来源: 题型:
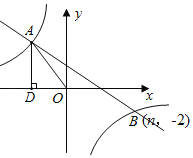
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一文具厂接到生产一批橡皮和水笔的任务,已知该文具厂销售200个橡皮和200个水笔的利润为160元,销售100个橡皮和200个水笔的利润为130元.已知该文具厂每天生产橡皮和水笔共4500个,生产橡皮和水笔每个成本分别为2元,3元,设每天生产橡皮![]() 个,该文具厂每天生产成本为
个,该文具厂每天生产成本为![]() 元.
元.
(1)求橡皮和水笔的销售单价;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若该文具厂每天最多投入成本为10000元,求该文具厂每天获得利润最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年全民抗疫期间,抗疫志士莫小贝购进一条生产线生产抗疫物质. 已知该生产线的三个操作平台分别排列在同一直线上,顺次是甲、乙、丙,其中甲乙平台之间的距离为40米,乙丙平台之间的距离为60米,操作甲、乙、丙平台分别需要20人、70人、60人. 由于时间仓促无法做到完全自动化,需要在三个平台之间建立一个原材料供给站让工人自取,有如下两个方案:方案一:让所有工人到供给站的距离总和最小;方案二:让甲、丙平台所有工人到供给站的距离之和等于乙平台所有工人到供给站的距离之和.
(1)若按照方案一建站,供给站距离甲平台多少米?
(2)若按照方案二建站,供给站距离甲平台多少米?
(3)在(2)的条件下,若甲平台的工人数增加![]() 人(
人(![]() ),那么随着
),那么随着![]() 的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
的增大,供给站将距离甲平台将越来越远,还是越来越近?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
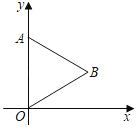
【题目】如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B的对应点B′的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.(0,﹣4)
D.(0,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙C过菱形ABCD的三个顶点B,A,D,连结BD,过点A作AE∥BD交射线CB于点E.
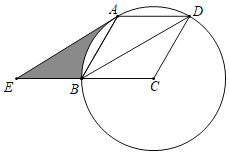
(1)求证:AE是⊙C的切线.
(2)若半径为2,求图中线段AE、线段BE和![]() 围成的部分的面积.
围成的部分的面积.
(3)在(2)的条件下,在⊙C上取点F,连结AF,使∠DAF=15°,求点F到直线AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
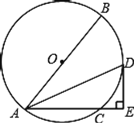
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)如果∠BAC=60°,AE=![]() ,求AC长.
,求AC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
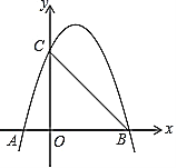
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在第一象限的抛物线上,连接
在第一象限的抛物线上,连接![]() ,
,![]() .试问,在对称轴左侧的抛物线是否存在一点
.试问,在对称轴左侧的抛物线是否存在一点![]() ,满足
,满足![]() ?如果存在,请求出点
?如果存在,请求出点![]() 的坐标:如果不存在,请明理由;
的坐标:如果不存在,请明理由;
(3)存在正实数![]() ,
,![]() (
(![]() ),当
),当![]() 时,恰好满足
时,恰好满足![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com