
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]() .
.![]()
![]() .
.![]() C.
C.![]() D.
D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在![]() 组中的数据是:94,90,94
组中的数据是:94,90,94
八年级抽取的学生竞赛成绩扇形统计图:
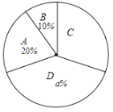
七、八年级抽取的学生竞赛成绩统计表:
年级 | 七年级 | 八年级 |
平均数 |
| 92 |
中位数 | 93 | 94 |
众数 | 99 | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校七、八年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(![]() )的学生人数是多少?
)的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)求证:AG与⊙O相切.
(2)若AC=6,AB=8,BE=3,求线段OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市将创建全国森林城市,提出了“共建绿色城”的倡议.某校积极响应,在3月12日植树节这天组织全校学生开展了植树活动,校团委对全校各班的植树情况道行了统计,绘制了如图所示的两个不完整的统计图.
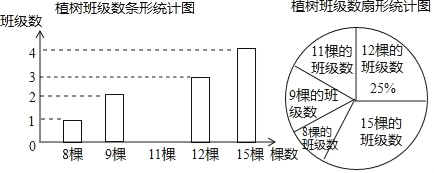
(1)求该校的班级总数;
(2)将条形统计图补充完整;
(3)求该校各班在这一活动中植树的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,……则第_____个图形中圆和正三角形的个数相等 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
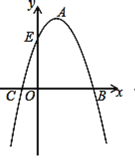
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点O是边AC的中点,分别过点A、C作射线BO的垂线,E、F是垂足.
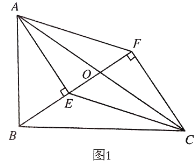
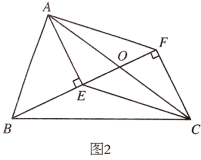
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2(k﹣1)x+2.
(1)当k=3时,求函数图象与x轴的交点坐标;
(2)函数图象的对称轴与原点的距离为2,当﹣1≤x≤5时,求此时函数的最小值;
(3)函数图象交y轴于点B,交直线x=4于点C,设二次函数图象上的一点P(x,y)满足0≤x≤4时,y≤2,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com