
【题目】下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,……则第_____个图形中圆和正三角形的个数相等 .

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】(模型介绍)
古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营![]() .他总是先去
.他总是先去![]() 营,再到河边饮马,之后,再巡查
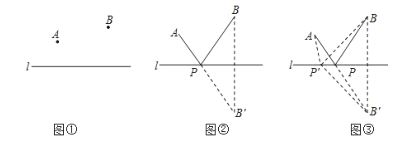
营,再到河边饮马,之后,再巡查![]() 营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点
营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连结
,连结![]() 与直线
与直线![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线
的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线![]() 上另取任一点
上另取任一点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,∵直线
,∵直线![]() 是点
是点![]() ,
,![]() 的对称轴,点
的对称轴,点![]() ,
,![]() 在
在![]() 上,
上,
(1)∴![]() __________,
__________,![]() _________,∴
_________,∴![]() ____________.在
____________.在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,即
,即![]() 最小.
最小.
(归纳总结)
在解决上述问题的过程中,我们利用轴对称变换,把点![]() 在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点
在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点![]() 为
为![]() 与
与![]() 的交点,即
的交点,即![]() ,
,![]() ,
,![]() 三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.
(模型应用)
(2)如图④,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 上一动点.求
上一动点.求![]() 的最小值.
的最小值.
解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点![]() 与
与![]() 关于直线
关于直线![]() 对称,连结
对称,连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的最小值就是线段
的最小值就是线段![]() 的长度,则
的长度,则![]() 的最小值是__________.
的最小值是__________.

(3)如图⑤,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂的最短路程为_________
处,则蚂蚁到达蜂的最短路程为_________![]() .
.

(4)如图⑥,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿射线
沿射线![]() 的方向平移,得到
的方向平移,得到![]() ,分别连接
,分别连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
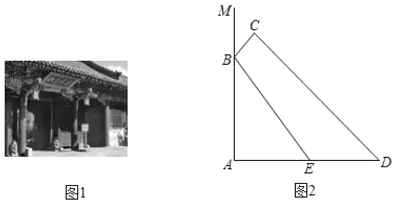
【题目】如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段![]() 就是悬挂在墙壁
就是悬挂在墙壁![]() 上的某块匾额的截面示意图.已知
上的某块匾额的截面示意图.已知![]() 米,
米,![]() .从水平地面点
.从水平地面点![]() 处看点
处看点![]() ,仰角
,仰角![]() ,从点
,从点![]() 处看点
处看点![]() ,仰角
,仰角![]() .且
.且![]() 米,求匾额悬挂的高度
米,求匾额悬挂的高度![]() 的长.(参考数据:
的长.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com