
【题目】如图所示,平行四边形内有两个全等的正六边形,若阴影部分的面积记为![]() ,平行四边形的面积记为
,平行四边形的面积记为![]() ,则
,则![]() 的值为____.
的值为____.
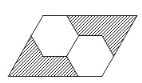
【答案】![]()
【解析】
如解图所示:延长EN交BC于点F,过点E作EP⊥BC于P,过点F作FQ⊥MN于Q,过点A作AD⊥BC于D,由图可知,图中两个阴影部分面积相等,证出△BEF为等边三角形,四边形NFGM为菱形,求出等边三角形的边长、菱形的边长和平行四边形的边长,利用锐角三角函数求出等边三角形的高、菱形的高和平行四边形的高,即可求出结论.
解:如下图所示,延长EN交BC于点F,过点E作EP⊥BC于P,过点F作FQ⊥MN于Q,过点A作AD⊥BC于D,
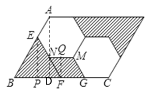
∵平行四边形内有两个全等的正六边形,设正六边形的边长为a
∴∠AEN=∠A=∠ENM=∠MGC=120°,NM∥BC,AE=EN=NM=MG=a
∴∠B=180°-∠A=60°,∠FNM=180°-∠ENM =60°,∠BEF=180°-∠AEN=60°,∠NFG=∠ENM=120°=∠MGC
∴∠B=∠BEF=60°,∠EFB=180°-∠NFG=60°,NF∥MG,
∴△BEF为等边三角形,四边形NFGM为菱形
∴NF=MG=a,
∴BE=BF=EF=EN+NF=2a,AB=AE+BE=3a,BC=BF+FG+GC=4a
∴EP=BE·sin∠B=![]() ,AD=AB·sin∠B=
,AD=AB·sin∠B=![]() ,FQ=NF·sin∠FNM=
,FQ=NF·sin∠FNM=![]()
由图可知,图中两个阴影部分面积相等
∴![]() =2(S△BEF+S菱形NFGM)
=2(S△BEF+S菱形NFGM)
=2(![]() BF·EP+NM·FQ)
BF·EP+NM·FQ)
=2(![]() ×2a×
×2a×![]() +a·
+a·![]() )
)
=![]()
![]() =BC·AD=4a×
=BC·AD=4a×![]() =
=![]()
∴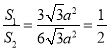
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
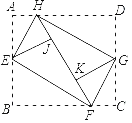
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
(3)如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.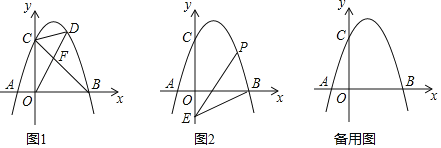
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,作
,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作圆.
为半径作圆.
(1)依据题意补充完整图形;(尺规作图,保留作图痕迹,不写作法)
(2)求证:![]() 与直线
与直线![]() 相切;
相切;
(3)在(2)的条件下,若![]() 与直线
与直线![]() 相切的切点为
相切的切点为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ;其中
;其中![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为_____.
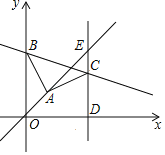
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,(为坐标原点,点![]() ,点
,点![]() 是
是![]() 中点,连接(
中点,连接(![]() 将
将![]() 绕点
绕点![]() 顺时针旋转,得到
顺时针旋转,得到![]() ,记旋转角为
,记旋转角为![]() ,点
,点![]() 的对应点分别是
的对应点分别是![]() ,连接
,连接![]() 是
是![]() 中点,连接
中点,连接![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;

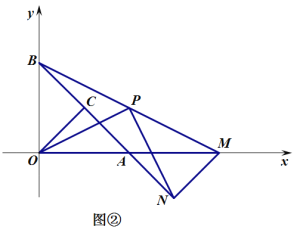
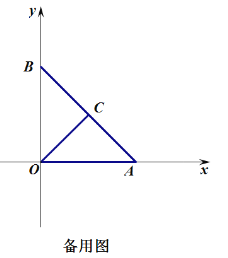
(2)如图②,当![]() 时,求证
时,求证![]() ,且
,且![]() ;
;
(3)当![]() 旋转至点
旋转至点![]() 共线时,求点
共线时,求点![]() 的坐标(直接写出结果即可) .
的坐标(直接写出结果即可) .
查看答案和解析>>
科目:初中数学 来源: 题型:
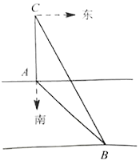
【题目】某数学活动小组实地测量某条河流两岸互相平行的一段东西走向的河的宽度.在河的北岸边点A处,测得河的南岸边点B处在其南偏东45°方向,然后向北走40米到达点C处,测得点B在点C的南偏东27°方向,求这段河的宽度.(结果精确到1米.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
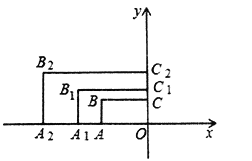
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
倍,得到矩形A2OC2B2,以此类推,得到的矩形A2020OC2020B2020的对角线交点的纵坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
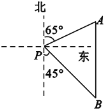
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,则这时海轮所在的B处距离灯塔P的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com