【题目】在直角坐标系中，(为坐标原点，点
，点
是
中点，连接(
将
绕点
顺时针旋转，得到
,记旋转角为
，点
的对应点分别是
,连接
是
中点，连接
．
（1）如图①，当
时，求点
的坐标；
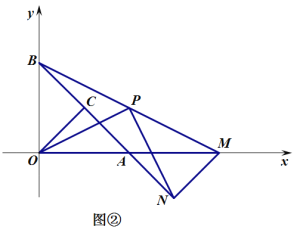
（2）如图②，当
时，求证
，且
；
（3）当旋转至点
共线时，求点的坐标(直接写出结果即可) ．
【答案】（1）点
；（2）见解析；（3）点
或
．
【解析】
（1）过点作
，垂足为
，由旋转图形性质，得到AM的长，再应用解直角三角形的知识问题可解；
（2）根据直角三角形斜边上中线等于斜边一半可证OP=PN，再由三角形内角和知识，证明
即可；
（3）根据题意画出满足条件图形，过M做
于点E，利用锐角三角函数和旋转的知识，求出
，则问题可解.
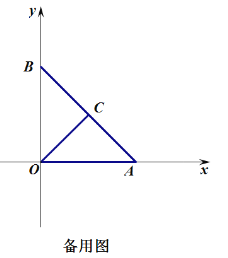
（1）如图
点
，点
是
中点
，
且
即
为等腰直角三角形
当
时，
点落在上，
由旋转可知
过点作，垂足为
则
则
点
如图，当
时，
点
共线，点
共线
，
且
是
中点，
，
且
则
可得
即
即
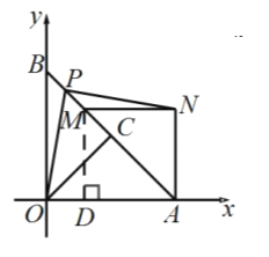
当点B、M、N共线，M位于B、N之间时，如图
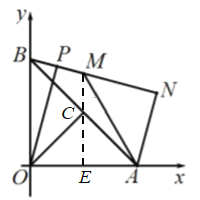
过M做于点E
由已知，
，
在
中，
在
中，
则点M坐标为
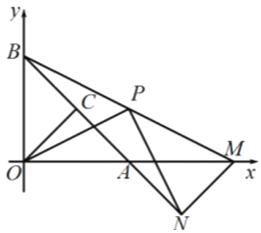
当点B、M、N共线，N位于B、M之间时，如图
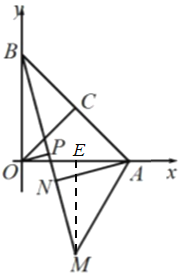
过M做于点E
由已知，，
在中，
在中，
则点M坐标为
综上，点或
科目：初中数学 来源： 题型：
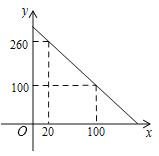
【题目】为了清洗水箱，需先放掉水箱内原有的存水，如图是水箱剩余水量y（升）随放水时间x（分）变化的图象．
（1）求y关于x的函数表达式，并确定自变量x的取值范围；
（2）若8：00打开放水龙头，估计8：55﹣9：10（包括8：55和9：10）水箱内的剩水量（即y的取值范围）；
（3）当水箱中存水少于10升时，放水时间至少超过多少分钟？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是平行四边形，AD与圆相切，请在下图中，仅用无刻度的直尺按要求画图.
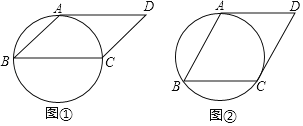
（1）若BC是圆的直径，画出平行四边形ABCD的边CD上的高；
（2）若CD与圆相切，画出平行四边形ABCD的边BC上的高AE.
查看答案和解析>>
科目：初中数学 来源： 题型：
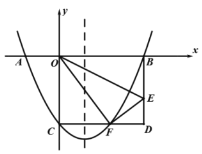
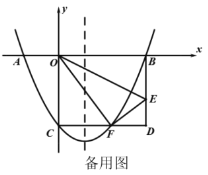
【题目】如图，在平面直角坐标系中，折叠矩形
的一边
，使点
落在
边的点
处，折痕为
，连接
．已知点
的坐标为
，二次函数
图象经过、
、三点．
（1）求函数解析式；
（2）在
轴下方抛物线上有一动点
，过点作
轴，交轴于点
，连接
，当
与
相似时，求点的坐标．
（3）在抛物线对称轴上是否存在一点
，使
有最大值？若存在，请直接写出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学号召全校学生进行安全教育网络学习，并对部分学生的学习情况进行了随机调查.对部分学生的成绩（x为整数，满分100分）进行统计，并绘制了如下统计图表．
调查结果频数分布表
| 调查结果扇形统计图
|
根据所给信息，解答下列问题：
（1）填空：
_________，
_________；
（2）求扇形统计图中，m的值及A组对应的圆心角的度数；
（3）若参加学习的同学共有1500人，请你估计成绩不低于80分的同学有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（ ）
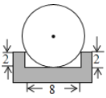
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）探究：
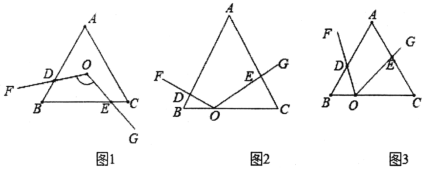
问题：如图1，等边三角形ABC的边长为6，点O是∠ABC和∠ACB的角平分线交点，∠FOG＝120°，绕点O任意旋转∠FOG，分别交△ABC的两边于D，E两点求四边形ODBE的面积．
讨论：
①甲：在∠FOG旋转过程中，当OF经过点B时，OG一定经过点C．
②乙：小明的分析有道理，这样，我们就可以利用“ASA”证出△ODB≌△OEC．
③丙：因为△ODB≌△OEC，所以只要算出△OBC的面积就得出了四边形ODBE的面积．
老师：同学们的思路很清晰，也很正确，在分析和解决问题时，我们经常会借用特例作辅助线来解决一般问题请你按照探究的思路，直接写出四边形ODBE的面积：________．
（2）应用：
①特例：如图2，∠FOG的顶点O在等边三角形ABC的边BC上，OB＝2，OC＝4，边OG⊥AC于点E，OF⊥AB于点D，求△BOD面积．
②探究：如图3，已知∠FOG＝60°，顶点O在等边三角形ABC的边BC上，OB＝2，OC＝4，记△BOD的面积为x，△COE的面积为y，求xy的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
