
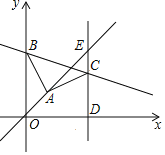
【题目】如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90°,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED=5EC,则直线BC解析式为_____.
【答案】y=﹣![]() x+10
x+10
【解析】
过A作AM⊥y轴,交y轴于M,交CD于N,证△ABM≌△CAN,推出AN=BM,CN=AM=4,设EC=a,ED=5a,求出a=2,得出B、C的坐标,设直线BC的解析式是y=kx+10,把C(10,8)代入求出直线BC的解析式.
解:过A作AM⊥y轴,交y轴于M,交CD于N,则∠BMA=∠ANC=90°,
∵∠BAC=90°,
∴∠BAM+∠CAN=90°,∠BAM+∠ABM=90°,
∴∠ABM=∠CAN,
∵A(4,4),
∴OM=DN=4,AM=4,
在△ABM和△CAN中,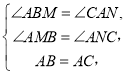
∴△ABM≌△CAN(AAS),
∴AN=BM,CN=AM=4,
∵ED=5EC,
∴设EC=a,ED=5a,
∵A(4,4),
∴点A在直线y=x上,
∵CN=4a﹣4,
则4a﹣4=4,
∴a=2,即CD=8,ED=10.
∵点E在直线y=x上,
∴E(10,10),
∴MN=10,C(10,8),
∴AN=BM=10﹣4=6,
∴B(0,10),
设直线BC的解析式是y=kx+10,
把C(10,8)代入得:k=﹣![]() ,
,
即直线BC的解析式是y=﹣![]() x+10,
x+10,
故答案为:y=﹣![]() x+10.
x+10.



科目:初中数学 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
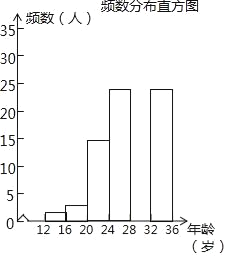
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x2<1,有下列结论:①b2﹣4ac>0;②4a﹣2b+c>﹣1;③﹣3<x1<﹣2;④当m为任意实数时,a﹣b≤am2+bm;⑤3a+c=0.其中,正确的结论有( )
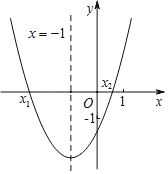
A.②③④B.①③⑤C.②④⑤D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
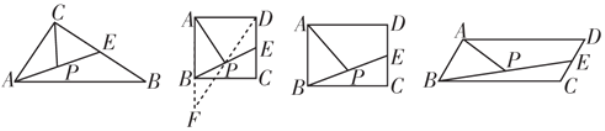
【题目】(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,则称CP是△ABC的“双中线”.若∠ACB=90°,AC=3,AB=5,则CP=________;
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”.若AB=4,则AP的长为__________;(按图示辅助线求解)
(3)在图3中,AP是矩形ABCD的“双中线”.若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(4)在图4中,AP是□ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°,求△ABP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
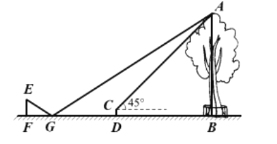
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
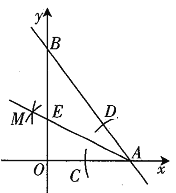
【题目】如图,![]() 的直角边
的直角边![]() 在x轴上,
在x轴上,![]() 在y轴的正半轴上,且
在y轴的正半轴上,且![]() ,
,![]() ,按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交
,按以下步骤作图:①以点A为圆心,适当长度为半径作弧,分别交![]() ,
,![]() 于点C,D;②分别以C,D为圆心,大于
于点C,D;②分别以C,D为圆心,大于![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点M;③作射线
内交于点M;③作射线![]() ,交y轴于点E,则点E的坐标为( )
,交y轴于点E,则点E的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
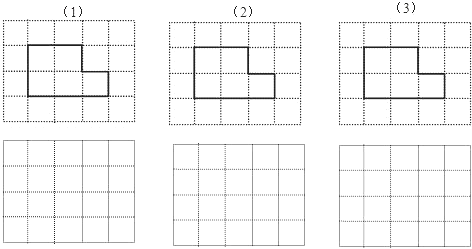
【题目】现有一块形如母子正方形的板材,木工师傅想先把它分割成几块,然后适当拼接,制成某种特殊形状的板面(要求板材不能有剩余,拼接时不重叠、无空隙),请你按下列要求,帮助木工师傅分别设计一种方案:
(1)板面形状为非正方形的中心对称图形;
(2)板面形状为等腰梯形;
(3)板面形状为正方形.
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面画出拼接后的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com